APTS Statistical Modelling
Model Selection
Professor of Statistics
Department of Statistics, University of Warwick
ioannis.kosmidis@warwick.ac.uk
ikosmidis.com ikosmidis ikosmidis_
22 April 2025
Housekeeping
Space, time and feedback
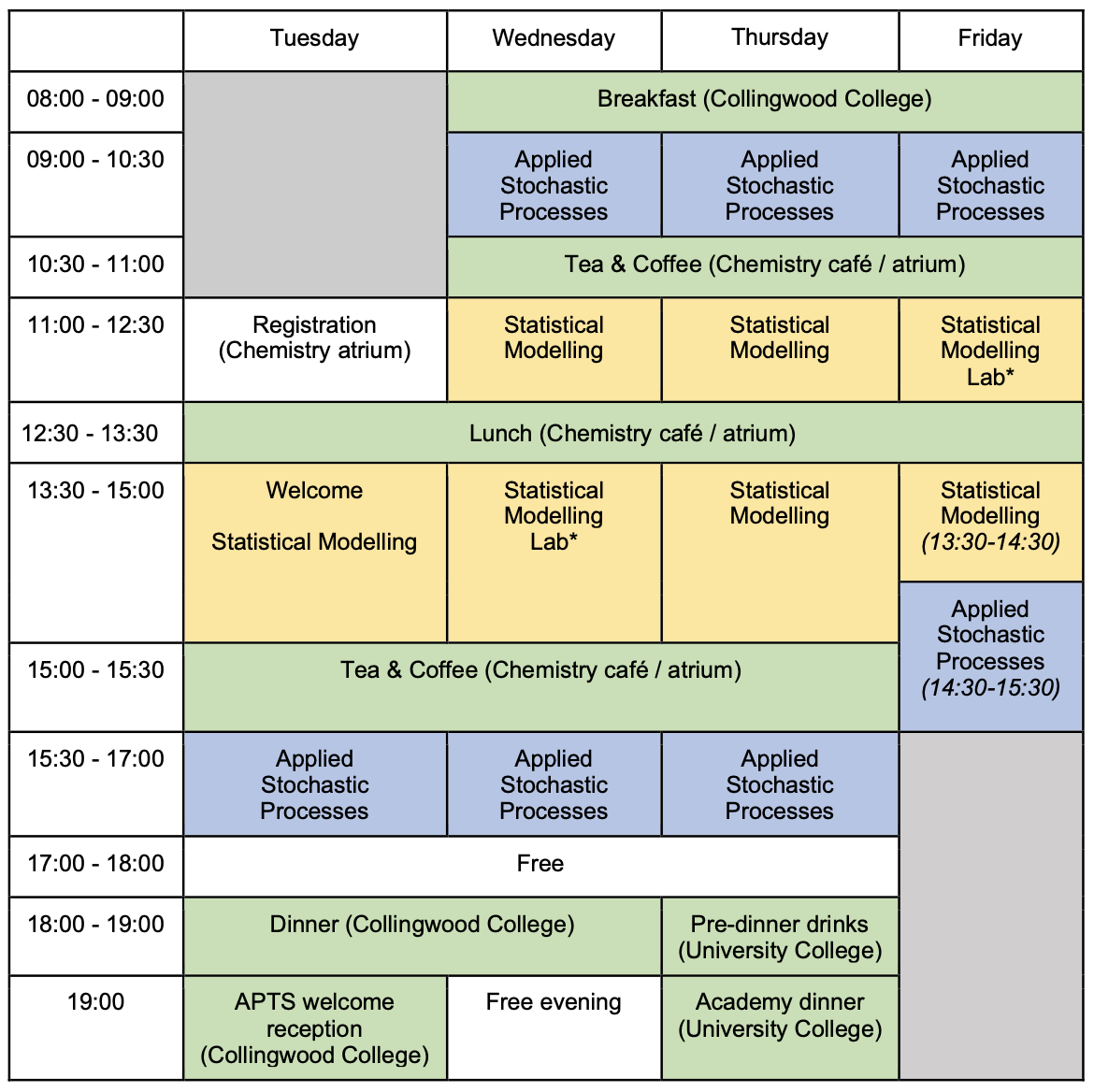
Rooms
| Room | Building | |
|---|---|---|
| Lectures, Labs | CG85 | Chemistry (15) |
| Breakouts rooms | PCL0501, /3-4, /6-9 | Palatine Centre |
| Lunch, Tea and coffee | Chemistry Cafe / Atrium | Chemistry (15) |
Feedback
Close to or after the end of the week, please make sure you provide your feedback at
Footnotes
Some slides have footnotes like1.
Footnotes have content that should not distract you as you skim through the slides but it is nevertheless important, including:
- Citations
- Commentary
- Exercises
Preliminary material, notes and slide decks
| Materials | Link |
|---|---|
| Preliminary material | ikosmidis.com/files/APTS-SM-Preliminary |
| Notes | ikosmidis.com/files/APTS-SM-Notes |
| Slides: Model selection 👀 | ikosmidis.com/files/APTS-SM-Slides-model-selection.html |
| Slides: Beyond GLMs | ikosmidis.com/files/APTS-SM-Slides-beyond-glms.html |
| Slides: Nonlinear models | ikosmidis.com/files/APTS-SM-Slides-nonlinear-models.html |
| Slides: Latent variables | ikosmidis.com/files/APTS-SM-Slides-latent.html |
| Lab 1 | ikosmidis.com/files/APTS-SM-Notes/lab1.html |
| Lab 2 | ikosmidis.com/files/APTS-SM-Notes/lab2.html |
Code-chunks
The R code reproducing the analyses and simulations presented on the slide deck is all embedded on the slides. Just click “[R Code]” wherever it appears.
For example,
From this point onward, when evaluating a code chunk, it is assumed that all previous chunks have been successfully evaluated.
R packages
The code on the slides rely on R version 4.5.0 (2025-04-11) and the packages
| package | version |
|---|---|
| dplyr | 1.1.4 |
| ggplot2 | 3.5.2 |
| mclust | 6.1.1 |
| MuMIn | 1.48.11 |
| SMPracticals | 1.4-3.1 |
| rgl | 1.3.18 |
| tidyr | 1.3.1 |
| cv | 2.0.3 |
You can load them (and install them if you do not have them already) by doing
Typos and other contributions
Let me know (either during the lectures or by email) if you find any tyops on the slides, or any of the other materials.
I would welcome contributions of code that replicates the analyses in the notes in other languages (e.g. Python, Julia).
Questions
I will be making time for questions.
Lift your hand or speak up at any point.
Principles
Model selection task
Select a statistical model from a set of candidate models on the basis of data.
Velocity of galaxies: ?MASS::galaxies
The velocities, in km/sec, of 82 galaxies, moving away from our own galaxy, from 6 well-separated conic sections of an ‘unfilled’ survey of the Corona Borealis region. Multimodality in such surveys is evidence for voids and superclusters in the far universe.
If galaxies are indeed super-clustered the distribution of their velocities estimated from the red-shift in their light-spectra would be multimodal, and unimodal otherwise.
R code
[1] 9172 9350 9483 9558 9775 10227 10406 16084 16170 18419 18552 18600
[13] 18927 19052 19070 19330 19343 19349 19440 19473 19529 19541 19547 19663
[25] 19846 19856 19863 19914 19918 19973 19989 20166 20175 20179 20196 20215
[37] 20221 20415 20629 20795 20821 20846 20875 20986 21137 21492 21701 21814
[49] 21921 21960 22185 22209 22242 22249 22314 22374 22495 22746 22747 22888
[61] 22914 23206 23241 23263 23484 23538 23542 23666 23706 23711 24129 24285
[73] 24289 24366 24717 24990 25633 26960 26995 32065 32789 34279Velocity of galaxies: ?MASS::galaxies
R code
## Rescale to 1000km/s
galaxies <- galaxies / 1000
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('bw = "nrd0"', 'bw = "SJ"'),
col = cols[2:3], lty = 1, lwd = 2)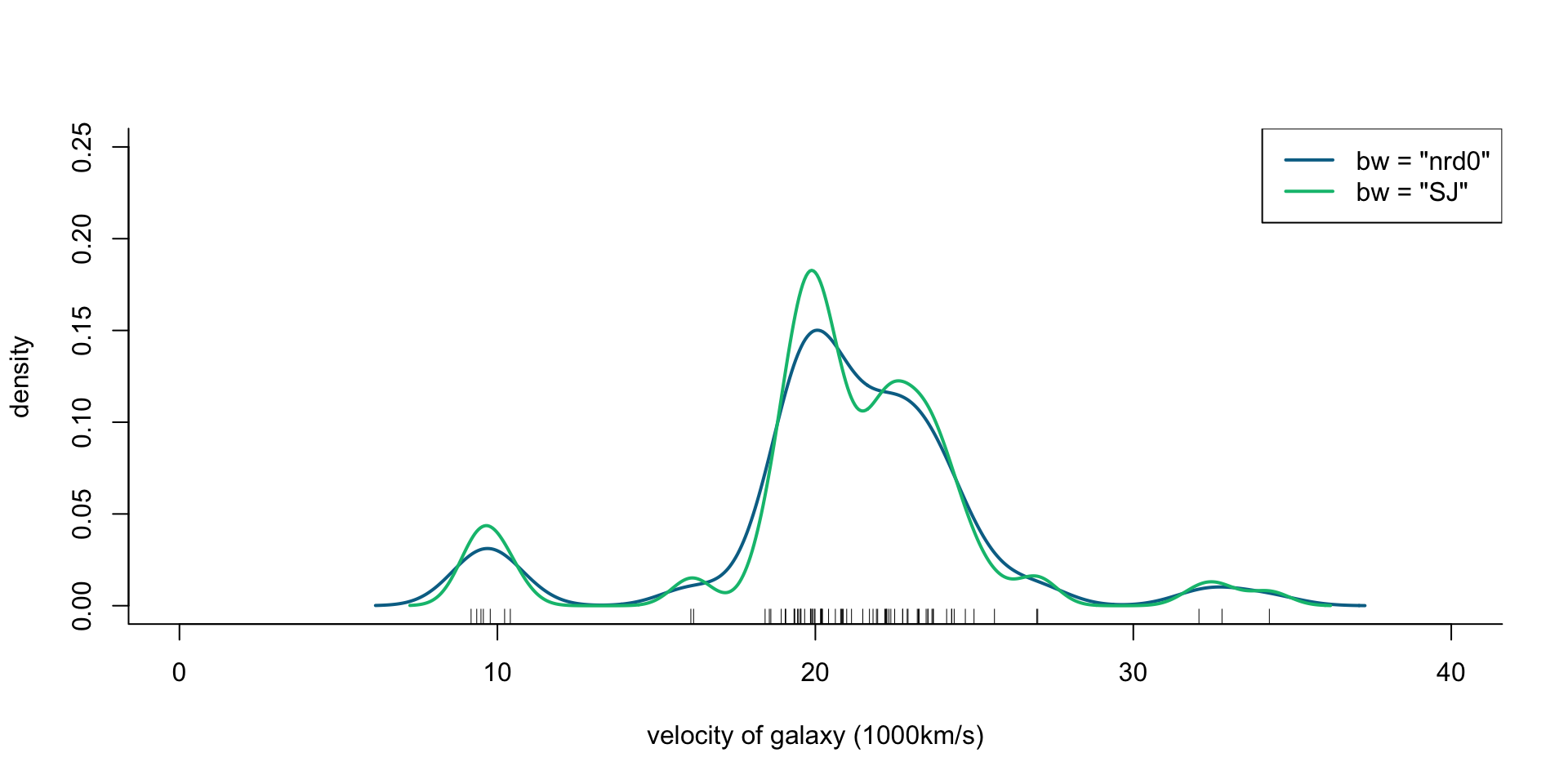
Figure 1: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures.
Velocity of galaxies: Mixture of normal distributions
The \(p\)-component gaussian mixture model has density \[ f(y \,;\,\pi, \theta) = \sum_{r=1}^p \pi_r \phi(y \,;\,\mu_r, \sigma_r^2) \quad (0\leq \pi_r\leq 1 \,;\,\sum_{r=1}^p \pi_r = 1) \] where \(\pi_r\) is the probability that \(y\) is from the \(r\)th component, and \(\phi(y \,;\,\mu_r, \sigma_r^2)\) is a normal density with component-specific mean \(\mu_r\) and variance \(\sigma_r^2\)
Set of candidate models
Any density with compact support support can be approximated by a gaussian mixture model1.
Gaussian mixture models with \(p \in \{1, 2, \ldots, \}\) components.
Velocity of galaxies: Model selection for density estimation
R code
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('GMM - 1 component', 'bw = "nrd0"', 'bw = "SJ"'),
col = cols, lty = 1)
ra <- seq(0, 40, length.out = 1000)
gal_mix <- Mclust(galaxies, G = 1, modelNames = "V")
lines(ra, dens(ra, modelName = "V", parameters = gal_mix$parameters),
col = cols[1], lwd = 2)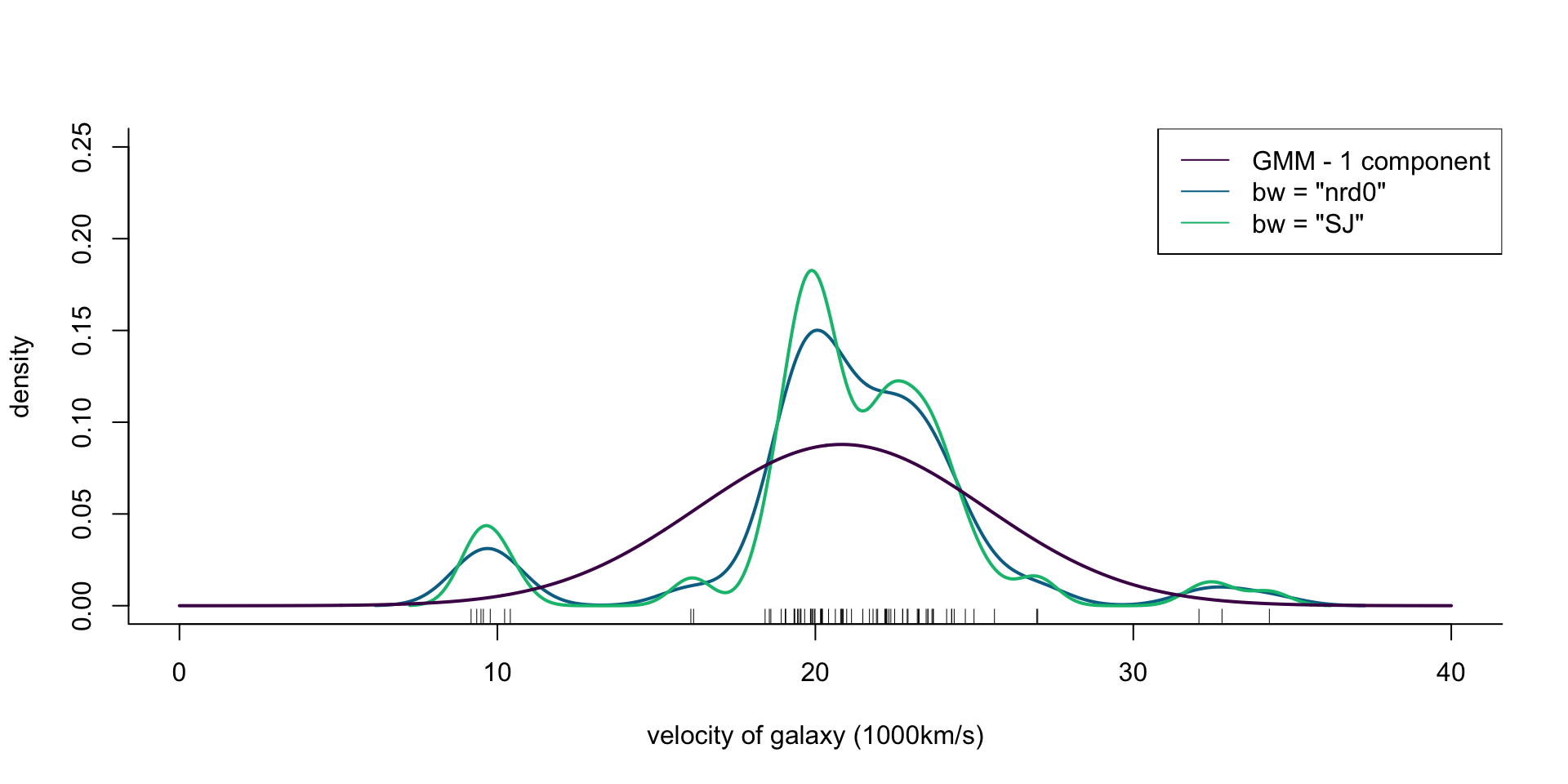
Figure 2: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures, and 1 normal density.
Velocity of galaxies: Model selection for density estimation
R code
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('GMM - 2 components', 'bw = "nrd0"', 'bw = "SJ"'),
col = cols, lty = 1)
ra <- seq(0, 40, length.out = 1000)
gal_mix <- Mclust(galaxies, G = 2, modelNames = "V")
lines(ra, dens(ra, modelName = "V", parameters = gal_mix$parameters),
col = cols[1], lwd = 2)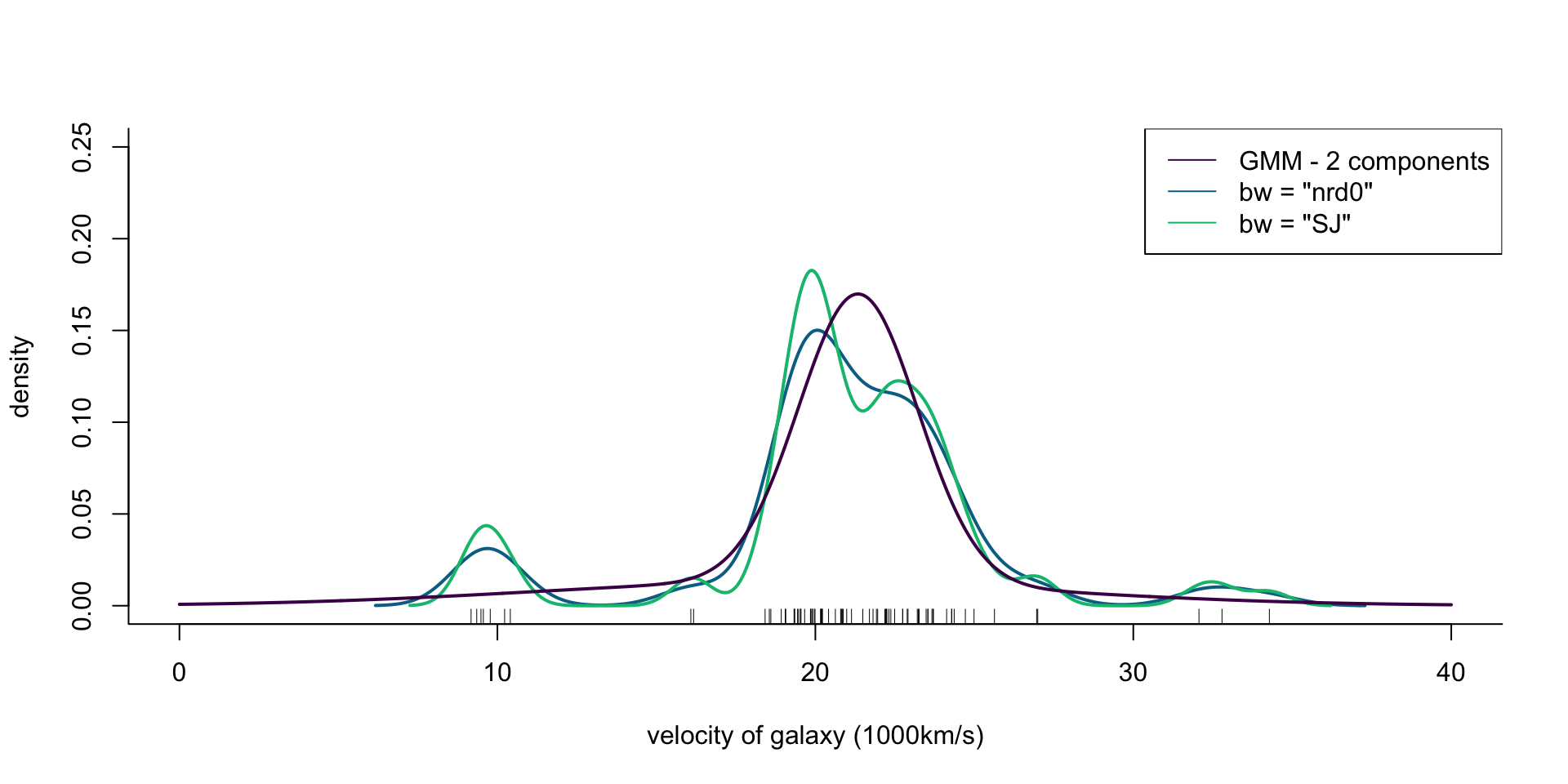
Figure 3: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures, and a mixture of 2 normal densities.
Velocity of galaxies: Model selection for density estimation
R code
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('GMM - 3 components', 'bw = "nrd0"', 'bw = "SJ"'),
col = cols, lty = 1)
ra <- seq(0, 40, length.out = 1000)
gal_mix <- Mclust(galaxies, G = 3, modelNames = "V")
lines(ra, dens(ra, modelName = "V", parameters = gal_mix$parameters),
col = cols[1], lwd = 2)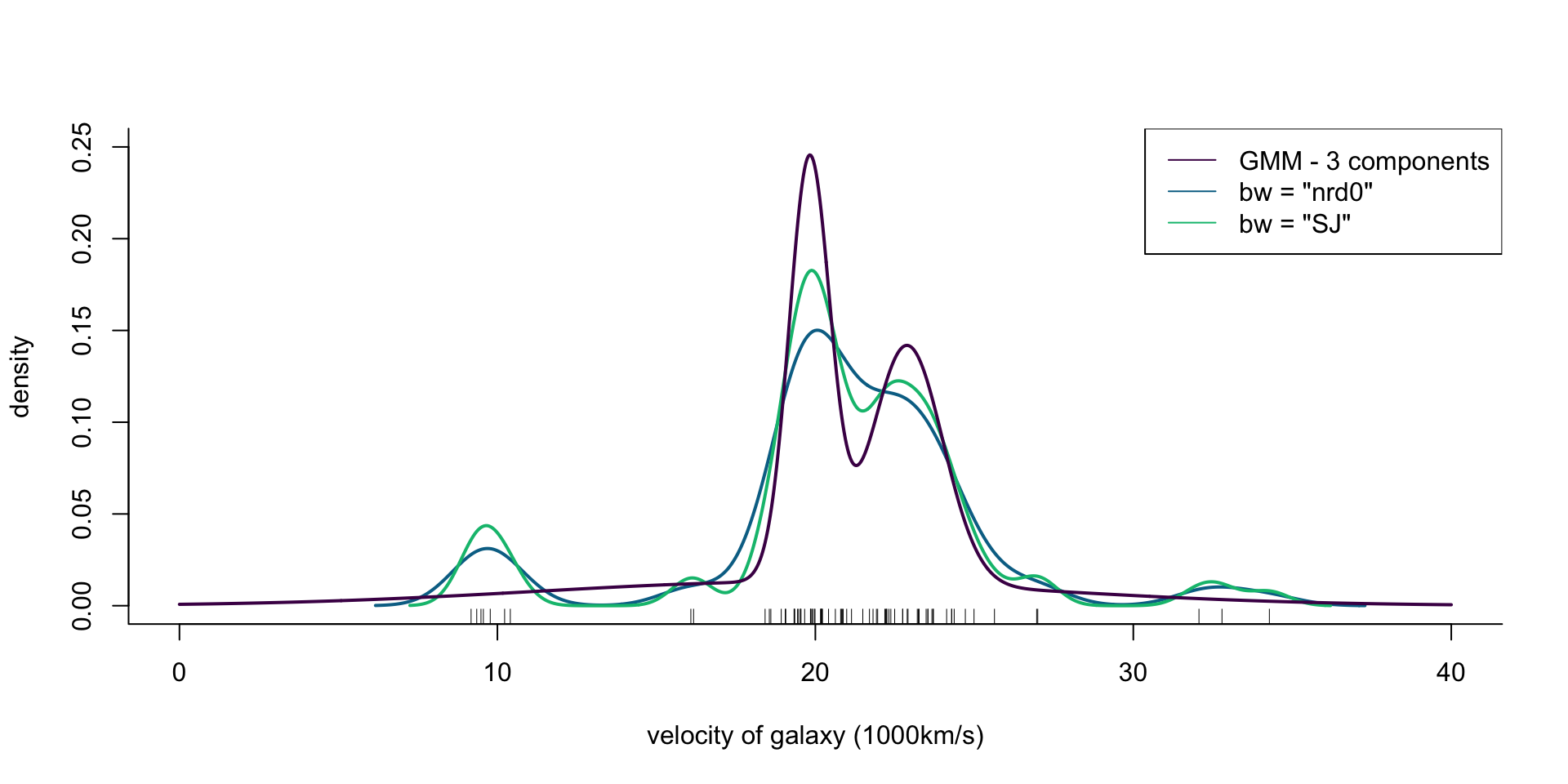
Figure 4: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures, and a mixture of 3 normal densities.
Velocity of galaxies: Model selection for density estimation
R code
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('GMM - 4 components', 'bw = "nrd0"', 'bw = "SJ"'),
col = cols, lty = 1)
ra <- seq(0, 40, length.out = 1000)
gal_mix <- Mclust(galaxies, G = 4, modelNames = "V")
lines(ra, dens(ra, modelName = "V", parameters = gal_mix$parameters),
col = cols[1], lwd = 2)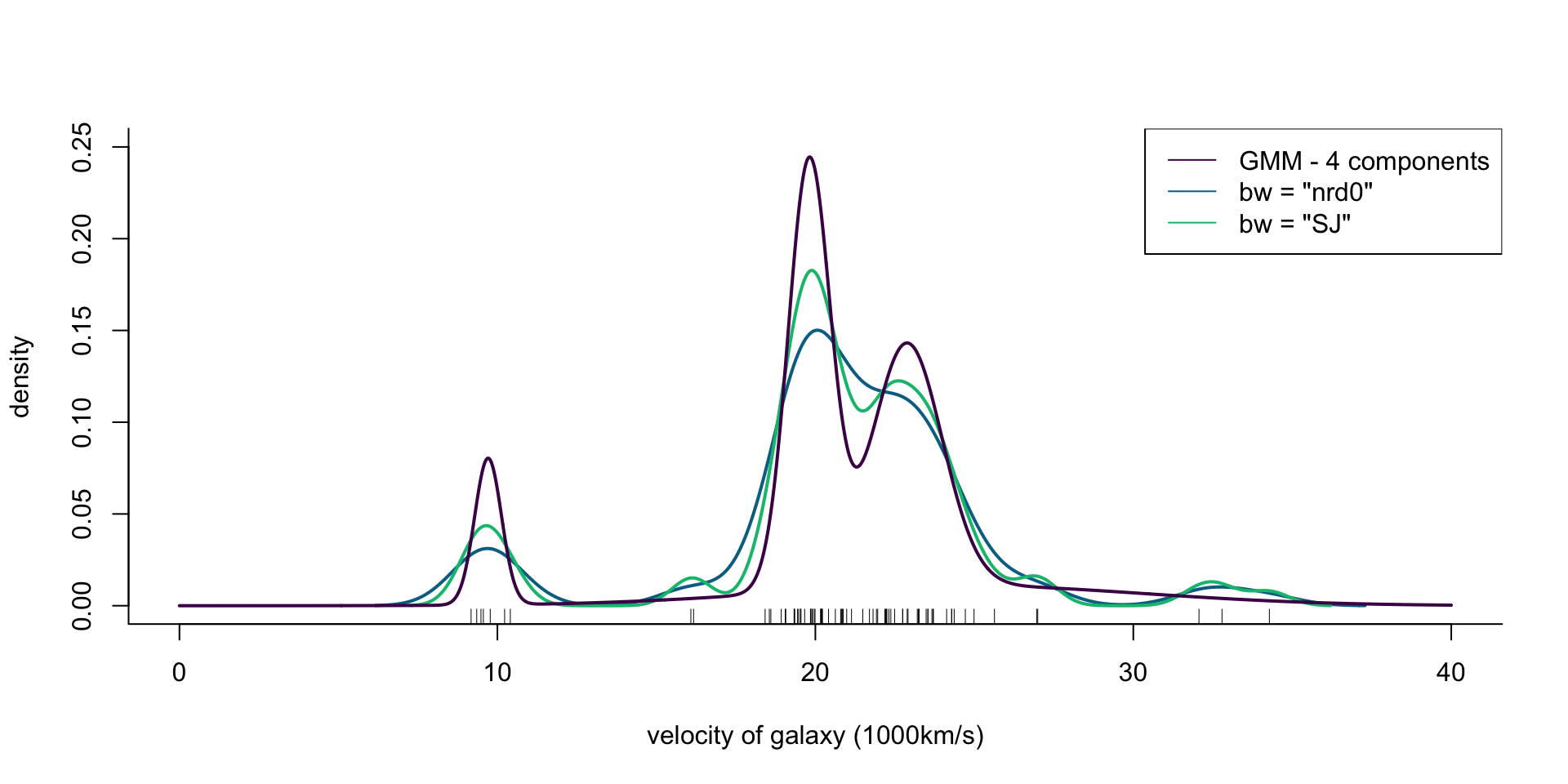
Figure 5: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures, and a mixture of 4 normal densities.
Velocity of galaxies: Model selection for density estimation
R code
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('GMM - 5 components', 'bw = "nrd0"', 'bw = "SJ"'),
col = cols, lty = 1)
ra <- seq(0, 40, length.out = 1000)
gal_mix <- Mclust(galaxies, G = 5, modelNames = "V")
lines(ra, dens(ra, modelName = "V", parameters = gal_mix$parameters),
col = cols[1], lwd = 2)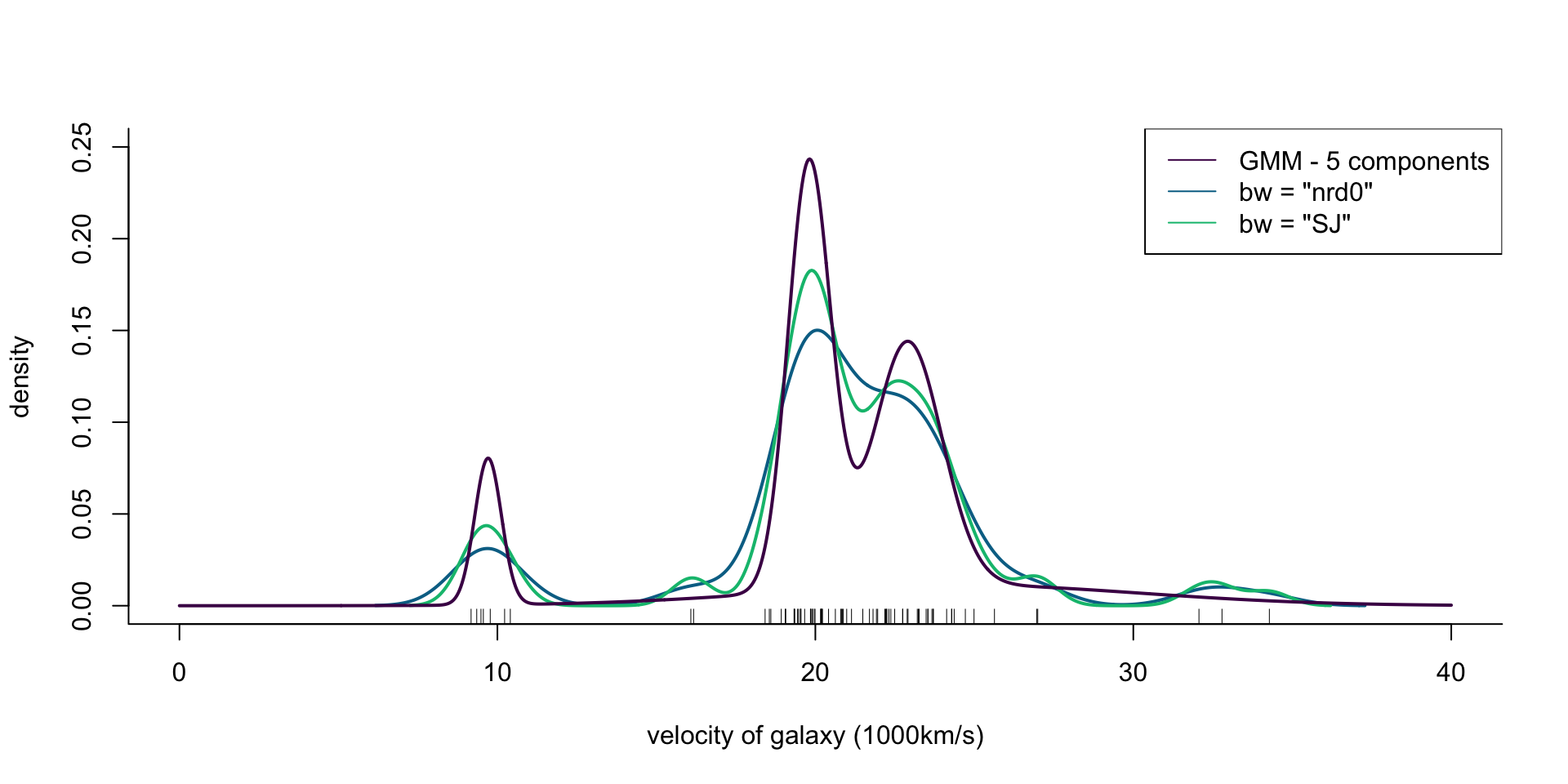
Figure 6: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures, and a mixture of 5 normal densities.
Velocity of galaxies: Model selection for density estimation
R code
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('GMM - 6 components', 'bw = "nrd0"', 'bw = "SJ"'),
col = cols, lty = 1)
ra <- seq(0, 40, length.out = 1000)
gal_mix <- Mclust(galaxies, G = 6, modelNames = "V")
lines(ra, dens(ra, modelName = "V", parameters = gal_mix$parameters),
col = cols[1], lwd = 2)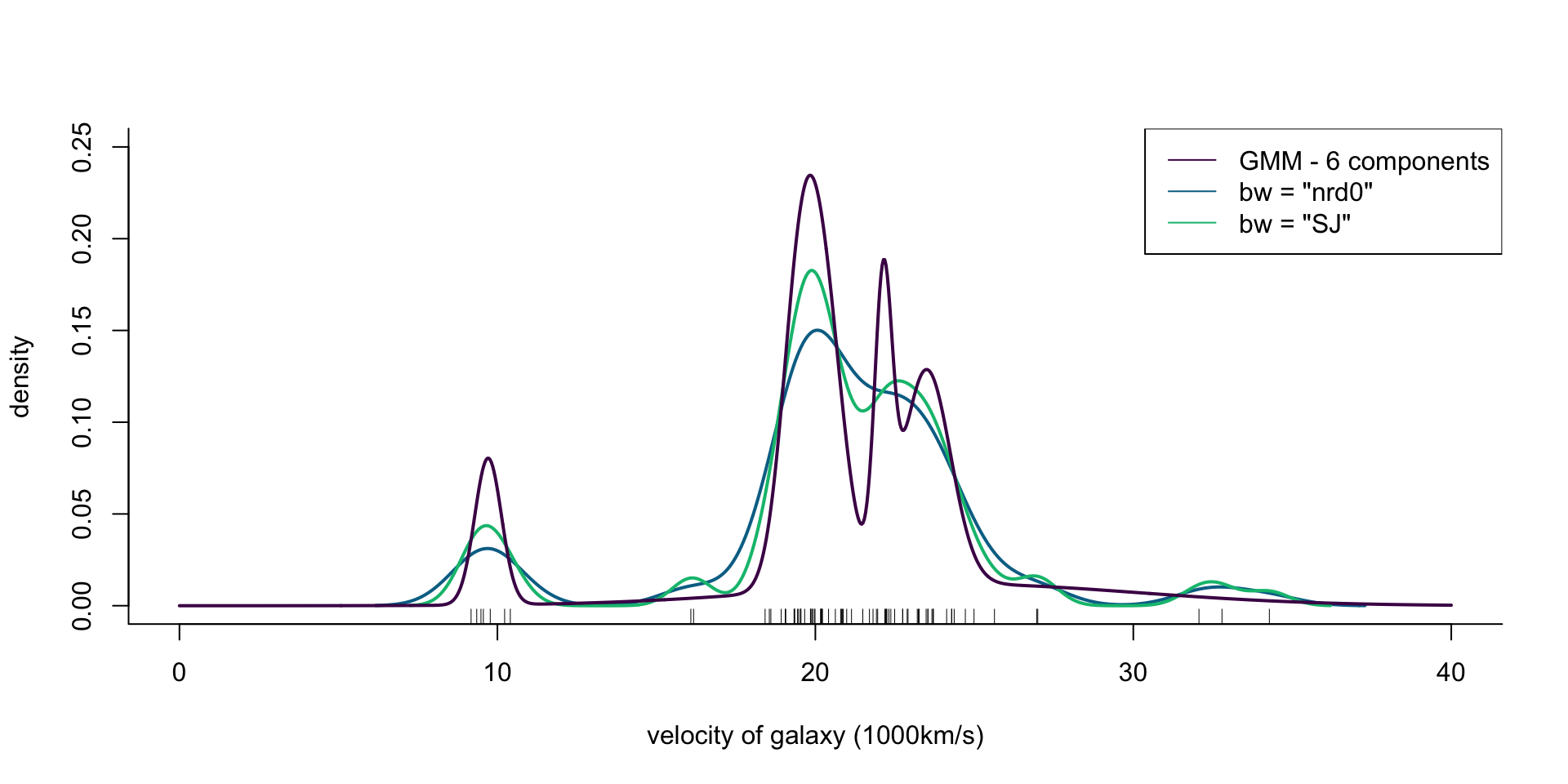
Figure 7: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures, and a mixture of 6 normal densities.
Velocity of galaxies: Model selection for density estimation
R code
plot(x = c(0, 40), y = c(0, 0.25), type = "n", bty = "l",
xlab = "velocity of galaxy (1000km/s)", ylab = "density")
rug(galaxies)
lines(density(galaxies, bw = "nrd0"), col = cols[2], lwd = 2)
lines(density(galaxies, bw = "SJ"), col = cols[3], lwd = 2)
legend("topright", legend = c('GMM - 7 components', 'bw = "nrd0"', 'bw = "SJ"'),
col = cols, lty = 1)
ra <- seq(0, 40, length.out = 1000)
gal_mix <- Mclust(galaxies, G = 7, modelNames = "V")
lines(ra, dens(ra, modelName = "V", parameters = gal_mix$parameters),
col = cols[1], lwd = 2)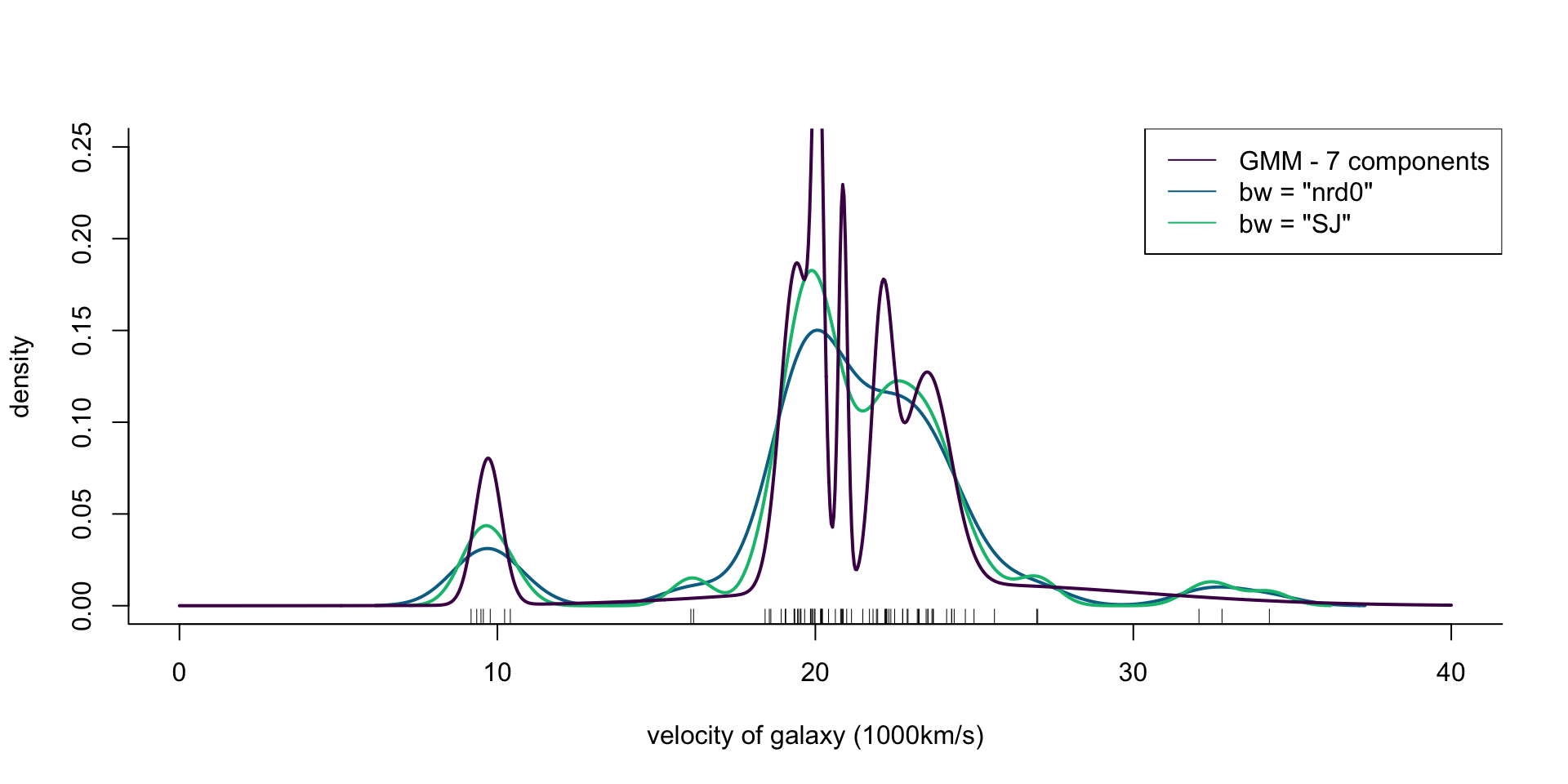
Figure 8: Density of galaxy velocities in 1000km/s, using two kernel density estimators with gaussian kernel but different bandwidth selection procedures, and a mixture of 7 normal densities.
Principles: Models are approximations
Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful. 1
Typically, there is no “correct” or “true” model, and even if there is one, it is often unknown and/or very complex. Of most practical value is to find and work with a simple model that performs well in some sense.
Principles: Bias-variance trade-off
Strike a balance between overfitting (too many parameters, model is unlikely to perform well out-of-sample) and underfitting (too few parameters, not capturing sufficient signal).
| Bias | Variance | |
|---|---|---|
| Simplicity | higher | lower |
| Complexity | lower | higher |
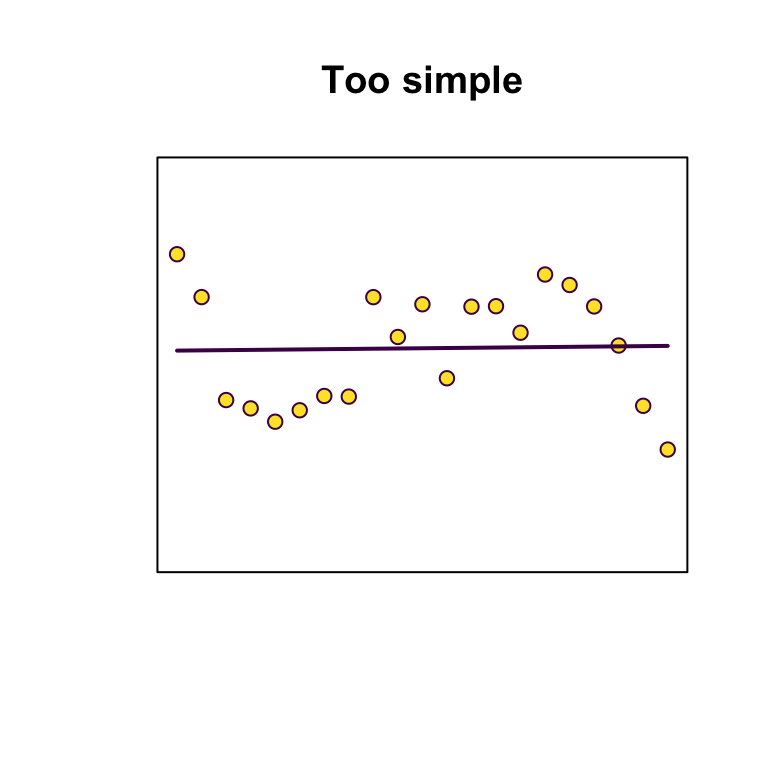
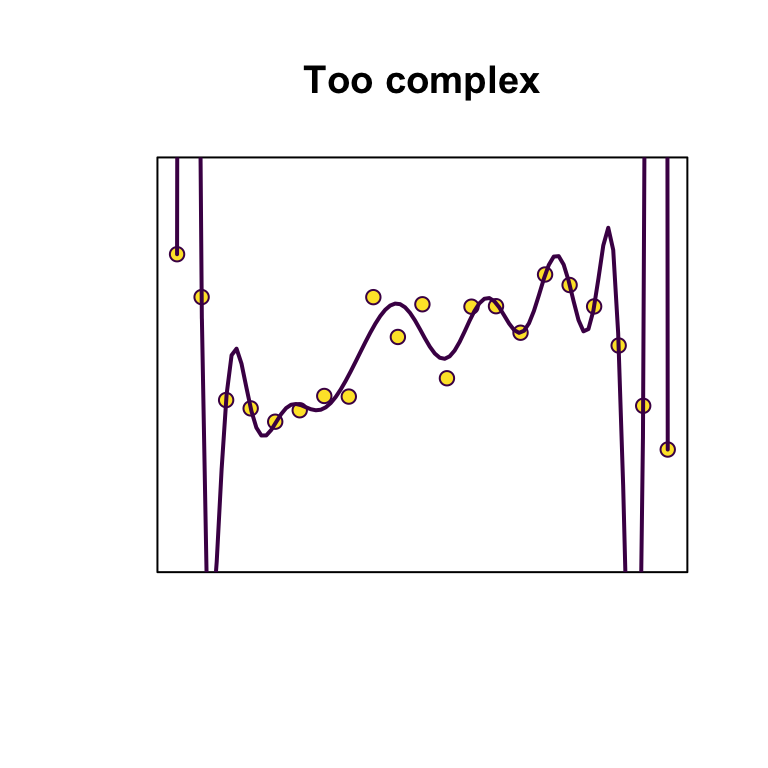
Principles: Parsimony
Only parameters that really matter for the particular aims of the analysis ought to be included in a selected model.
Principles: Context and focus
How odd it is that anyone should not see that all observation must be for or against some view if it is to be of any service.
All modelling is rooted in a specific scientific context and serves a particular purpose.
Different researchers may interpret the same data differently, and different scientific schools may have varying preferences for modelling and data analysis aims.
The purpose of models can vary, ranging from prediction and classification to deeper understanding of the underlying model1 to learning specific quantities well.
Model selection in regression
Regression models
Data
Response vectors \(y_1, \ldots, y_n\), with \(y_i \in \Re^m\)
Covariate vectors \(x_1, \ldots, x_n\), with \(x_i = (x_{i1}, \ldots, x_{ip})^\top \in \Re^{p}\)
Regression model
Conditional distributions with density or probability mass function \[ f(y_1, \ldots, y_n \mid x_1, \ldots, x_n \,;\,\psi, \lambda) \] where \(\psi = h(\beta, x_1, \ldots, x_n)\)
Sets of candidate models
Depending on the application and aims of the analysis, sets of candidate models can be constructed by:
varying the distributional assumption; and/or
varying aspects of \(\lambda\); and/or
varying aspects of \(\psi\)
Variable selection
Linear combinations of parameters and covariates
Many well-used regression models have \(\psi = h(X \beta)\), where \(X\) is a model matrix with rows \(x_1, \ldots, x_n\) (e.g. generalized linear models, generalized linear mixed effects models, generalized additive models, etc.).
Variable selection
A commonly required data-analytic task is variable selection, which is the identification of the best subset of columns of \(X\) either for predictive or explanatory purposes.
The appropriate set of candidate models is then of the kind 3, and consists of models defined by considering some or all possible subsets of columns of \(X\) in \(h(X \beta)\).
\(\beta_{s_1} = \ldots = \beta_{s_j} = 0\), \(s_i \in \{1, \ldots, p\}\) \(\sim\) drop columns \(s_1, \ldots, s_j\) from \(X\)
Complexity of variable selection
If columns of \(X\) correspond to single dimensional features, then it is tempting to consider all \(2^p\) subsets of columns of \(X\). But,
\(p = 10\) \(\implies\) about a thousand models
\(p = 20\) \(\implies\) about a million models
\(p = 30\) \(\implies\) about a billion models
Principles for candidate sets of models in variable selection
Principle of marginality
Unless substantive knowledge dictates otherwise,
If an interaction is present, then keep all respective main effects.
If a higher-order term is present (e.g. \(x^3\)), then keep all lower-order terms (e.g. \(x\) and \(x^2\)).
Keep the intercept parameter in.
1, 3 are essential for explanatory modelling, and all 1-3 avoid some very specific models. e.g.
R code
set.seed(123)
x <- seq(-10, 10, length.out = 100)
y <- 10 + 3 * x + 0.25 * x^2 + rnorm(100, 0, 10)
forms <- c(y ~ x, y ~ x + I(x^2), y ~ I(x^2), y ~ -1 + x, y ~ -1 + x + I(x^2), y ~ -1 + I(x^2))
df <- NULL
for (f in forms) {
df <- rbind(df, data.frame(x = x, y = y, yhat = predict(lm(f)), model = deparse(f)))
}
df <- df |> transform(model = factor(model, levels = sapply(forms, deparse), ordered = TRUE))
ggplot(df) +
geom_point(aes(x, y), pch = 21, fill = cols[4]) +
geom_line(aes(x, yhat), size = 1, col = cols[1]) +
facet_grid(~ model) +
theme_minimal() +
theme(legend.position = "none", axis.ticks = NULL)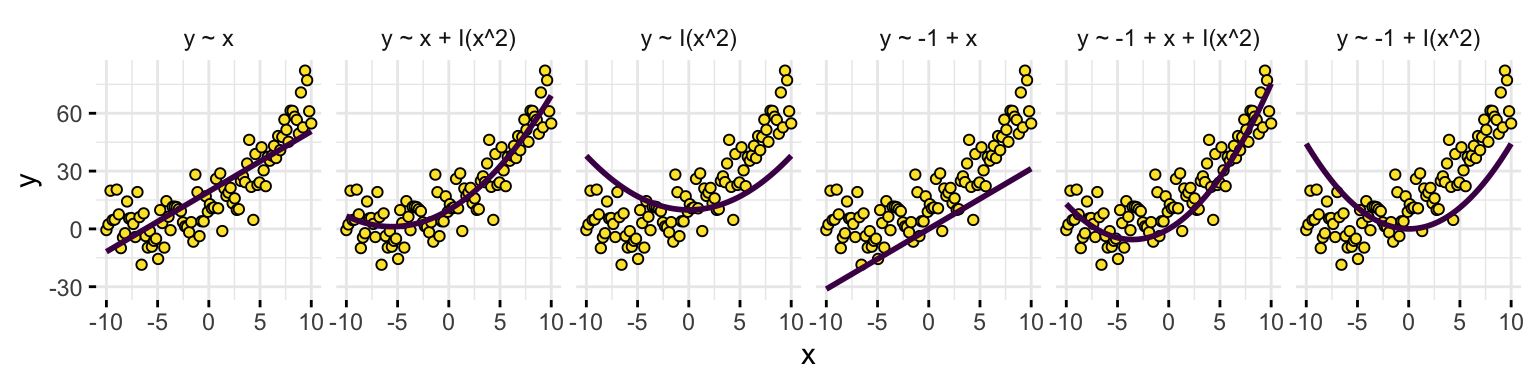
Principles for candidate sets of models in variable selection
Inclusion or removal of structurally grouped covariates
A prime example of structurally grouped covariate are qualitative covariates, which are typically represented as dummy variables. e.g.
\[ T \in \{\text{taxi}, \text{bus}, \text{train}\} \]
\[\sim\]
\[ x_{\rm taxi} = \left\{ \begin{array}{ll} 1 \,, & \text{if } T = \text{taxi}\\ 0 \,, & \text{otherwise}\\ \end{array} \right. \,, x_{\rm bus} = \left\{ \begin{array}{ll} 1 \,, & \text{if } T = \text{bus}\\ 0 \,, & \text{otherwise}\\ \end{array} \right. \,, x_{\rm train} = \left\{ \begin{array}{ll} 1 \,, & \text{if } T = \text{train}\\ 0 \,, & \text{otherwise}\\ \end{array} \right. \]
It is natural, and essential for explanatory modelling, to select or omit the whole group of variables encoding a qualitative covariate.
Aliasing should be accounted for if an intercept parameter is in the model (e.g. dropping one of the dummy variables, hence setting a reference category).
Logistic regression
Data
Response values \(y_1, \ldots, y_n\), with \(y_i \in \{0, 1\}\)
Covariate vectors \(x_1, \ldots, x_n\), with \(x_i = (x_{i1}, \ldots, x_{ip})^\top \in \Re^p\)
Model
\(Y_{1}, \ldots, Y_{n}\) conditionally independent with
\[ Y_i \mid x_i \sim \mathop{\mathrm{Bernoulli}}(\mu_i)\,, \quad \log \frac{\mu_i}{1 - \mu_i} = \eta_i = \sum_{t = 1}^p \beta_t x_{it} \]
Widely used for inference about covariate effects on probabilities, probability calibration, and prediction.
i.e. \(f(y_1, \ldots, y_n \mid x_1, \ldots, x_n \,;\,\psi, \lambda) = \prod_{i} f(y_i \mid x_i \,;\,\psi_i)\) with \(f(y_i \mid x_i \,;\,\psi_i)\) the Bernoulli pmf with probability \(\psi_i = \mu_i = (1 + \exp(-\eta_i))^{-1}\).
Logistic regression log-likelihood
\[ \ell(\beta) = \sum_{i=1}^n y_i x_i^\top \beta - \sum_{i=1}^n \log\left\{1 + \exp( x_i^\top \beta)\right\} \]
We expect a good fit to be one that gives large maximized log-likelihood \(\hat \ell = \ell(\hat\beta)\) where \(\hat\beta\) is the maximum likelihood estimator
Nodal involvement: ?SMPracticals::nodal
The treatment strategy for a patient diagnosed with cancer of the prostate depends highly on whether the cancer has spread to the surrounding lymph nodes.
It is common to operate on the patient to get samples from the nodes which are then analysed under a microscope.
For a sample of 53 prostate cancer patients, a number of possible predictor variables were measured before surgery. The patients then had surgery to determine nodal involvement.
Rows: 53
Columns: 7
$ m <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ r <dbl> 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0…
$ aged <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0…
$ stage <fct> 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0…
$ grade <fct> 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0…
$ xray <fct> 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ acid <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0…For variable descriptions, hover over the words below
m r aged stage grade xray acid
Nodal involvement
Considering only the models with an intercept and without any interaction between the 5 binary covariates, results in \(2^5 = 32\) possible logistic regression models for this data.
R code
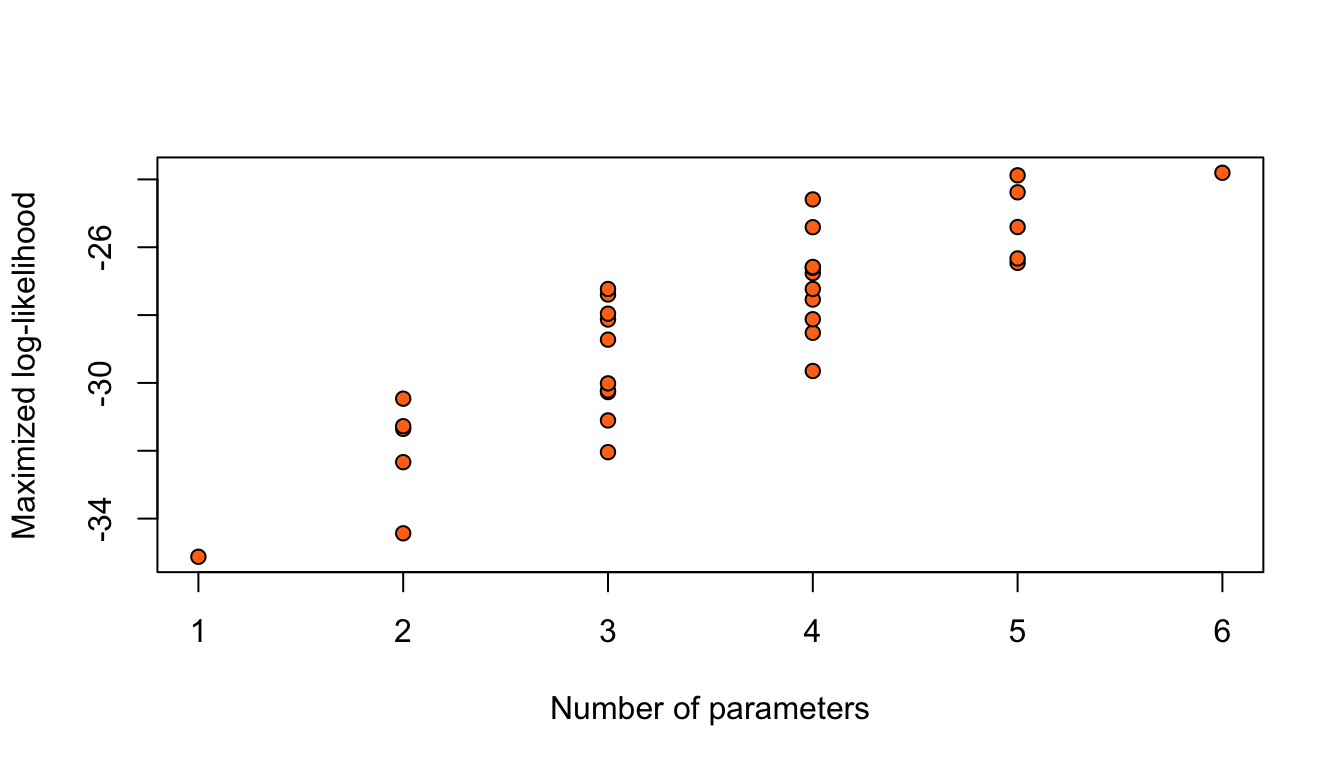
Figure 9: Maximized log-likelihoods for 32 possible logistic regression models for the nodal data.
Adding terms always increases the maximized log-likelihood.
Simply, taking the model with highest \(\hat\ell\) would give the model with all parameters.
Linear regression
Data
Response values \(y_1, \ldots, y_n\), with \(y_i \in \Re\)
Covariate vectors \(x_1, \ldots, x_n\), with \(x_i = (x_{i1}, \ldots, x_{ip})^\top \in \Re^p\)
Model
\[ Y_i = \eta_i = \sum_{t = 1}^p \beta_t x_{it} + \epsilon_i \] where \(\mathop{\mathrm{E}}(\epsilon_i) = 0\) and \(\mathop{\mathrm{var}}(\epsilon_i) = \sigma^2 < \infty\)
i.e. \(\psi_i = \mathop{\mathrm{E}}(Y_i \mid x_i) = \eta_i\) and \(\lambda = \sigma^2\)
Linear regression
Same issues as logistic regression when model selection is based on the residual sum of squares \(\|y - \hat{\eta} \|_2^2\). Removing terms always increases \(\|y - \hat{\eta} \|_2^2\).
Variable selection with linear models
Data
\(n\)-vector of responses \(y = (y_1, \ldots, y_n)^\top\)
\(n \times p_*\) matrix \(X_*\) with \(j\)th column \(v_j\), \(j \in \mathcal{I}= \{1, \ldots, p_*\}\)
True relationship between \(y\) and \(X\)
\(Y = \mu + \epsilon = X_\heartsuit \beta_\heartsuit + \epsilon\)
\(X_\heartsuit\) is an \(n \times p_\heartsuit\) matrix with columns \(\{v_j : j \in \mathcal{J}\subseteq \mathcal{I}\}\), \(|\mathcal{J}| = p_\heartsuit \le p_*\)
Aim
Estimate \(\mathcal{J}\) based on data
Variable selection with linear models
Candidate model
\(Y = X\beta + \epsilon\) where \(X\) consists of the columns of \(X_*\) with indices in \(\mathcal{S}\subseteq \mathcal{I}\), \(|\mathcal{S}| = p \le p_*\)
Types of selected models
| Type | Selected set \(\mathcal{S}\) |
|---|---|
| Correct | \(\mathcal{J}\subseteq \mathcal{S}\subseteq \mathcal{I}\) |
| Wrong | \(\mathcal{S}\not\subset \mathcal{J}\) |
| True | \(\mathcal{J}\) |
Expected prediction error
One approach to select a candidate model is to minimize the expected prediction error \[ \Delta = n^{-1} {\mathop{\mathrm{E}}} \left[{\mathop{\mathrm{E}}}^+\left\{ \|Y^+ - X\hat\beta\|_2^2 \right\}\right] \] across the set of candidates models, where \(Y^+ = \mu + \epsilon^{+}\), with \(\epsilon^+\) an independent copy of \(\epsilon\), and expectation \({\mathop{\mathrm{E}}}(\cdot)\) is with respect to \(Y\) and \({\mathop{\mathrm{E}}}^+(\cdot)\) with respect to \(Y^+\).1
Bias / Variance trade-off
The fitted values from the candidate model are \[ X\hat\beta = X \{ (X^\top X)^{-1}X^\top Y\} = H\mu + H\epsilon \] where \(H = X (X^\top X)^{-1} X^\top\) is the hat matrix. Then,1
\[ \begin{aligned} \|Y^{+} - X\hat\beta\|_2^2 & = \mu^\top (I_n - H) \mu + (\epsilon^{+})^\top \epsilon^{+} + \epsilon^\top H \epsilon + Z \end{aligned} \]
where \(Z\) collects all terms with \({\mathop{\mathrm{E}}}[{\mathop{\mathrm{E}}}^{+}(Z)] = 0\). From the assumptions on the errors, we have \({\mathop{\mathrm{E}}}[{\mathop{\mathrm{E}}}^{+}((\epsilon^{+})^\top \epsilon^{+})] = n \sigma^2\), and \({\mathop{\mathrm{E}}}[{\mathop{\mathrm{E}}}^{+}(\epsilon^\top H \epsilon)] = \mathop{\mathrm{tr}}{H}\sigma^2 = p\sigma^2\). Collecting terms
Prediction mean squared error
\[ \Delta = \underbrace{\mu^\top (I_n - H) \mu / n}_{\text{Bias}^2} + \overbrace{(1 + p / n) \sigma^2}^{\text{Variance}} \]
Bias / Variance trade-off
| Type | Selected set \(\mathcal{S}\) | \(\Delta\) |
|---|---|---|
| Wrong | \(\mathcal{S}\not\subset \mathcal{J}\) | \(\mu^\top (I_n - H) \mu / n + (1 + p / n) \sigma^2\) |
| Correct | \(\mathcal{J}\subseteq \mathcal{S}\subseteq \mathcal{I}\) | \((1 + p / n) \sigma^2\), \(p \ge p_\heartsuit\) |
| True | \(\mathcal{J}\) | \((1 + p_\heartsuit / n) \sigma^2\) |
Bias
\(n^{-1}\mu^\top (I_n - H) \mu = n^{-1}\|\mu - H\mu\|_2^2 \ge 0\), and zero only if the model is correct (\(H\mu = \mu\))
Bias is reduced the closer \(\mu\) is to the space spanned by the columns of \(X\)
We expect a reduction in bias when useful covariates are added to the model
Variance
\((1 + p/n) \sigma^2\) increases as \(p\) increases, for example whenever useless terms are included
Polynomial regression
True model
\[ Y_i = \sum_{j = 0}^{5} x_i^j + \epsilon_i \] \(\mu_i = \sum_{j = 0}^{5} x_i^j\) is a degree five polynomial
Candidate models
\[ Y_i = \sum_{j = 0}^{p - 1} \beta_j x_i^j + \epsilon_i \quad (i = 1, \ldots, n)\, , \]
\(x_1, \ldots, x_n\) generated from \(n\) independent \(\mathop{\mathrm{N}}(0, 1)\)
Polynomial regression
\(n = 20\)
R code
Delta <- function(p, p0, x, sigma2) {
cols <- 0:(p - 1)
cols0 <- 0:(p0 - 1)
n <- length(x)
X <- matrix(rep(x, p)^rep(cols, each = n), nrow = n)
X0 <- matrix(rep(x, p0)^rep(cols0, each = n), nrow = n)
mu <- rowSums(X0)
H <- tcrossprod(qr.Q(qr(X)))
bias <- sum(((diag(n) - H) %*% mu)^2) / n
variance <- sigma2 * (1 + p / n)
c(p = p, bias = bias, variance = variance)
}
n <- 20
sigma2 <- 2
p_max <- 15
p0 <- 6
set.seed(1)
x <- rnorm(n)
D <- data.frame(t(sapply(1:p_max, Delta, p0 = p0, x = x, sigma2 = 1)))
par(mfrow = c(1, 3))
plot(bias ~ p, data = D, subset = p > 3,
main = expression("Bias"^2), ylab = "",
type = "b", bg = cols[1], pch = 21)
abline(v = p0, lty = 3, col = "grey")
plot(variance ~ p, data = D, subset = p > 3,
main = expression("Variance"), ylab = "",
type = "b", bg = cols[2], pch = 21)
abline(v = p0, lty = 3, col = "grey")
plot(bias + variance ~ p, data = D, subset = p > 3,
main = expression(Delta), ylab = "",
type = "b", bg = cols[3], pch = 21)
abline(v = p0, lty = 3, col = "grey")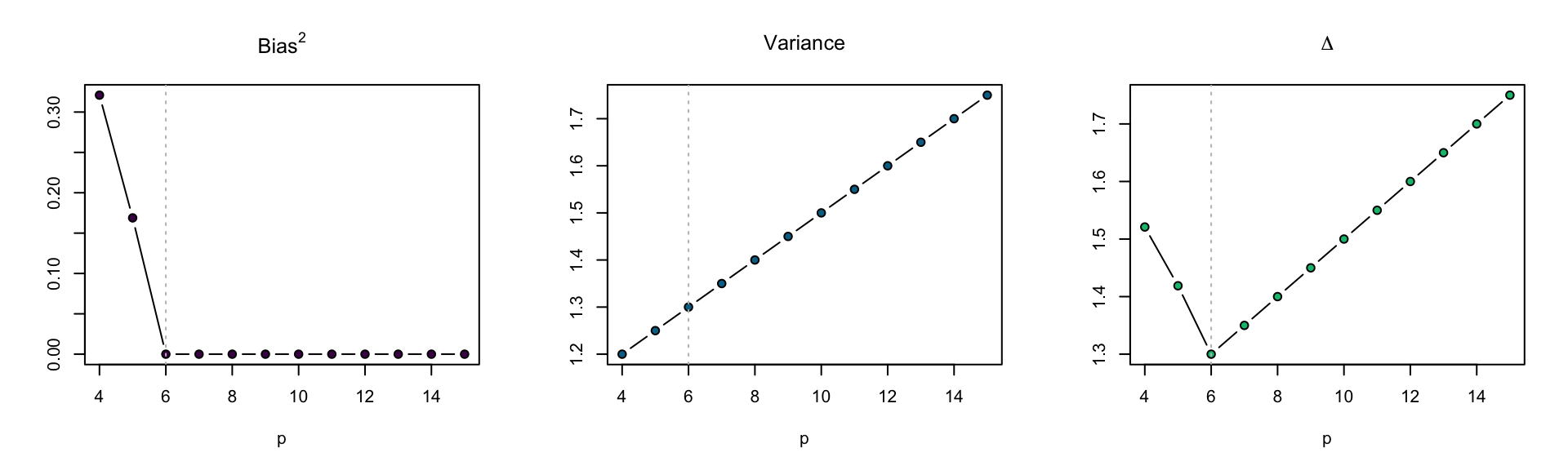
Figure 10: \(\Delta\) for models with varying polynomial degree.
AIC and TIC
Setting
True model
Independent \(Y_1, \ldots, Y_n\), where \(Y_i\) has a density function \(g(y)\).
Candidate model1
Independent \(Y_1, \ldots, Y_n\), where \(Y_i\) has a density function \(f(y \,;\,\theta)\).
There may be no value of \(\theta\) such that \(f(\cdot \,;\,\theta) = g(\cdot)\).
Maximized log-likelihood as a model selection criterion
Jensen’s inequality implies1 \[ {\mathop{\mathrm{E}}}_g \left[ \log g(y) \right] \ge {\mathop{\mathrm{E}}}_g\left[ \log f(y \,;\,\theta) \right] \tag{1}\] where \({\mathop{\mathrm{E}}}_g\) denotes expectation with respect to the density \(g(\cdot)\). The two expectations are equal if and only if \(f(y \,;\, \theta) = g(y)\).
Best approximating (aka “least false”) parameter value
\[ \theta_g = \arg \max_\theta {\mathop{\mathrm{E}}}_g \left[ \log f(y \,;\,\theta) \right] \]
If there is a parameter value \(\theta_0\) such that \(g(y) = f(y \,;\,\theta_0)\), then \(\theta_g = \theta_0\).
Maximized log-likelihood as a model selection criterion
An approach to model selection would be to maximize an estimate of \({\mathop{\mathrm{E}}}_g \left[ \log f(y \,;\,\theta) \right]\) over the set of candidate models, with one such an estimate being \[ \bar\ell(\hat\theta) = n^{-1} \sum_{i = 1}^n \log f(y_i \,;\,\hat\theta) \]
However, by definition of \(\hat\theta\), \(\bar\ell(\hat\theta) \ge \bar\ell(\theta_g)\). So, \(\bar\ell(\hat\theta)\) is biased upwards.
Nodal involvement
Considering only the models with an intercept and without any interaction between the 5 binary covariates, results in \(2^5 = 32\) possible logistic regression models for this data.
R code
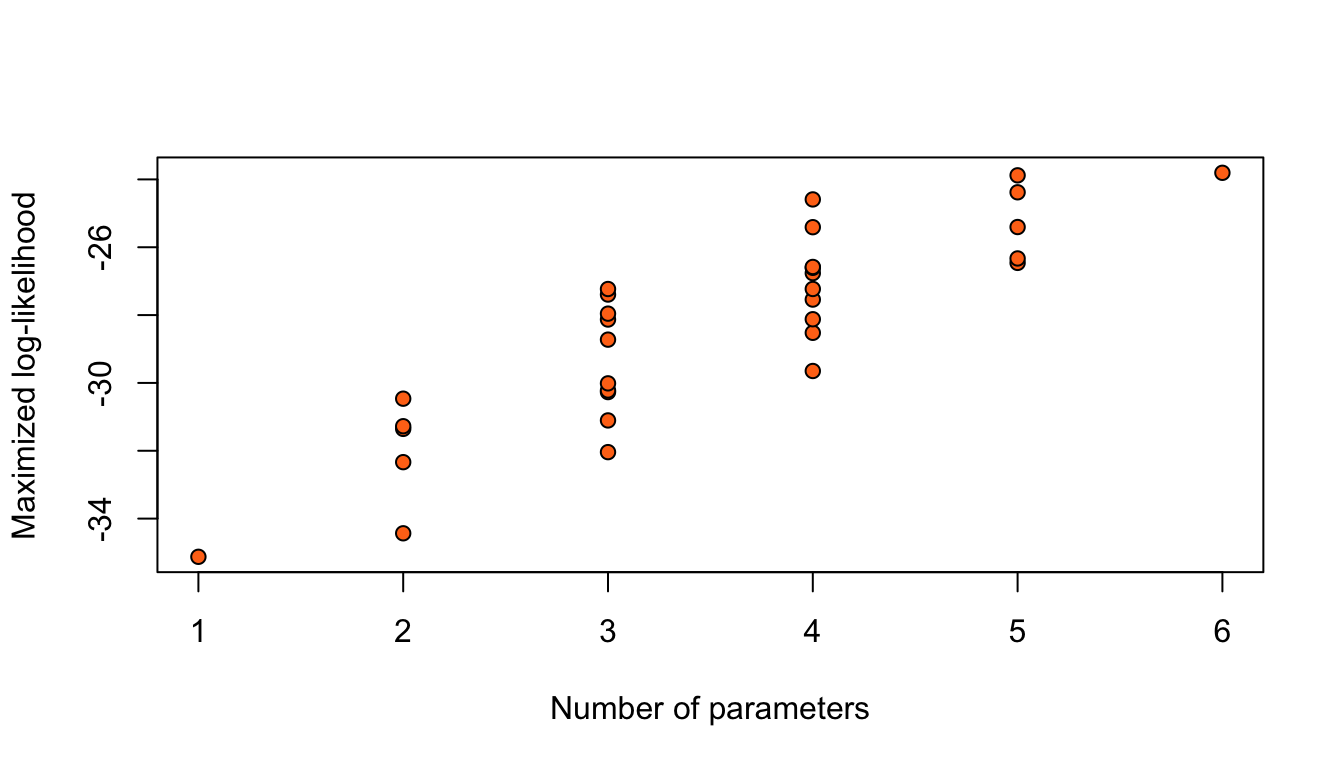
Figure 11: Maximized log-likelihoods for 32 possible logistic regression models for the nodal data.
Adding terms always increases the maximized log-likelihood.
Simply, taking the model with highest \(\hat\ell\) would give the model with all parameters.
Some results: Kullback-Leibler divergence
The log-likelihood \(\ell(\theta)\) of the candidate model is maximized at \(\hat\theta\), and \[ \bar \ell(\hat\theta) = n^{-1}\ell(\hat\theta) \to \int \log f(y \,;\,\theta_g) g(y)\, dy, \quad \text{as } n\to\infty \] where \(\theta_g\) minimizes the Kullback-Leibler divergence \[ KL(f_\theta,g) = \int \log\left\{ \frac{g(y)}{f(y \,;\,\theta)}\right\} g(y) \, dy \]
\(\theta_g\) gives the density \(f(y \,;\,\theta_g)\) closest to \(g(y)\), in this sense.
Some results: Inference under model misspecification
Asymptotic distribution of \(\hat\theta\)
Under mild regularity conditions, the maximum likelihood estimator \(\hat\theta\) satisfies \[ \sqrt{n} (\hat\theta - \theta_g) \stackrel{\text{d}}{\longrightarrow}{\mathop{\mathrm{N}}}\left( 0, n I(\theta_g)^{-1}K(\theta_g)I(\theta_g)^{-1}\right) \tag{2}\] where \[ \begin{aligned} K(\theta) &= n \int \frac{\partial \log f(y \,;\,\theta)}{\partial\theta} \frac{\partial \log f(y \,;\,\theta)}{\partial\theta^\top }g(y)\, dy,\\ I(\theta) &= - n \int \frac{\partial^2 \log f(y \,;\,\theta)}{\partial\theta\partial\theta^\top } g(y)\, dy \end{aligned} \]
Some results: Inference under model misspecification
Likelihood ratio statistic
The likelihood ratio statistic converges in distribution as \[ W(\theta_g)=2\left\{\ell(\hat\theta)-\ell(\theta_g)\right\} \stackrel{d}{\rightarrow} \sum_{r=1}^p \lambda_r V_r \] where \(V_1, \ldots, V_p\) are independent with \(V_i \sim \chi^2_1\), and \(\lambda_r\) are eigenvalues of \(K(\theta_g)^{1/2}I(\theta_g)^{-1} K(\theta_g)^{1/2}\).
Thus, \(E\{W(\theta_g)\} \rightarrow \mathop{\mathrm{tr}}\{I(\theta_g)^{-1}K(\theta_g)\}\).
Some results: Inference under model misspecification
Estimating \(K(\theta_g)\) and \(I(\theta_g)\)
In practice, \(g(y)\) is, of course, unknown, and \(K(\theta_g)\) and \(I(\theta_g)\) are estimated by \[ \hat K = \sum_{i=1}^n \frac{\partial \log f(y_i \,;\,\hat\theta)}{\partial\theta} \frac{\partial \log f(y_i \,;\,\hat\theta)}{\partial\theta^\top }, \quad \underbrace{\hat J = - \sum_{i=1}^n \frac{\partial^2 \log f(y_i \,;\,\hat\theta)} {\partial\theta\partial\theta^\top }}_{\text{observed information}} \]
Asymptotically valid inference
We can construct inferences about \(\theta_g\), using the fact that the approximate distribution of \(\hat\theta\) is \({\mathop{\mathrm{N}}}\left( \theta_g, I(\theta_g)^{-1}K(\theta_g)I(\theta_g)^{-1}\right)\), replacing the variance covariance matrix with \(\hat J^{-1}\hat K\hat J^{-1}\).
Maximum likelihood asymptotics under the true model
If \(g(\theta) = f(y \,;\,\theta_0)\), then \(\theta_0 = \theta_g\), \(K(\theta_g) = I(\theta_g)\) and \(\lambda_1 = \ldots = \lambda_p = 1\), and we recover the usual results.
Some results: Inference under model misspecification
Delta method
Suppose that \(\phi(\theta)\) is a smooth scalar transformation of the model parameters that is of particular interest, and let \(\phi'(\theta) = \nabla \phi(\theta)\). It holds that \[ \sqrt{n} \left(\phi(\hat\theta) - \phi(\theta_g)\right) \stackrel{\text{d}}{\longrightarrow}N(0, \sigma^2_\phi(\theta_g)) \, \] with \(\sigma^2_\phi(\theta) = n \{\phi'(\theta)\}^\top I(\theta)^{-1} K(\theta) I(\theta)^{-1} \phi'(\theta)\).
Some results: Inference under model misspecification
A blueprint for asymptotically valid inference
These results are general and valid for all smooth models (even the ones you might develop during your PhD) under rather mild regularity conditions
For ML inference you need:
The ML estimator \(\hat\theta\);
The observed information matrix \(\hat{J} = J(\hat\theta)\) with \(J(\theta) = -\nabla \nabla^\top \ell(\theta)\);
An estimate \(\hat{K}\) of \(K(\theta_g)\);1
\(\nabla \phi(\theta)\) if you have a focus parameter \(\phi(\theta)\).
The same blueprint also applies to general \(M\)-estimators (e.g. quasi likelihood methods, generalized estimating equations, composite likelihood methods, etc.) 2
Out-of-sample prediction
Problems with using \(\bar\ell(\hat\theta)\) for model selection:
- Upward bias, as \(\bar\ell(\hat\theta) \ge \bar\ell(\theta_g)\) because \(\hat\theta\) is based on \(Y_1, \ldots, Y_n\)
- Improves quality of fit with no control over model complexity
If we had another independent sample \(Y_1^+,\ldots,Y_n^+\sim g\) and computed \[ \bar\ell^+(\hat\theta) = n^{-1}\sum_{i=1}^n \log f(Y^+_i \,;\,\hat\theta) \] then both problems disappear. In the limit, we can choose the candidate model that maximizes \[ \Delta = {\mathop{\mathrm{E}}}_g\left[ {\mathop{\mathrm{E}}}^+_g\left\{ \bar\ell^+(\hat\theta) \right\} \right] \] where the inner expectation is over the distribution of \(Y_i^+\), and the outer expectation is over the distribution of \(\hat\theta\).
Bias of \(\bar \ell(\hat \theta)\) as an estimator of \(\Delta\)
\[ {\mathop{\mathrm{E}}}_g\{\bar \ell(\hat \theta)\} - \Delta = \underbrace{{\mathop{\mathrm{E}}}_g\{\bar \ell(\hat \theta) - \bar \ell(\theta_g)\}}_{a} + \underbrace{{\mathop{\mathrm{E}}}_g\{\bar \ell(\theta_g)\} - \Delta}_{b} \]
From the asymptotic distribution of \(W(\theta_g)\) \[ \begin{aligned} a & = {\mathop{\mathrm{E}}}_g\{\bar\ell(\hat\theta) - \bar\ell(\theta_g)\} \\ & = \frac{1}{2n}E_g\{W(\theta_g)\} \\ & \approx \frac{1}{2n}\mathop{\mathrm{tr}}\{I(\theta_g)^{-1} K(\theta_g)\} \end{aligned} \]
A Taylor expansion of \(\bar\ell^+(\hat\theta)\) around \(\theta_g\) and results on inference under the wrong model can be used to show that1 \[ \begin{aligned} b & = {\mathop{\mathrm{E}}}_g\{\bar \ell(\theta_g)\} - \Delta \\ & \approx \frac{1}{2n} \mathop{\mathrm{tr}}\{I(\theta_g)^{-1} K(\theta_g)\} \end{aligned} \]
\[\Large\Downarrow\]
\[ {\mathop{\mathrm{E}}}_g\{\bar \ell(\hat \theta)\} - \Delta \approx \mathop{\mathrm{tr}}\{I(\theta_g)^{-1} K(\theta_g)\} / n \]
Takeuchi information criterion
We can reduce the bias of \(\bar\ell(\hat\theta)\) as an estimator \(\Delta\) by using the corrected estimator \[ \bar\ell(\hat\theta) - \frac{1}{n}\mathop{\mathrm{tr}}(\hat J^{-1} \hat K) \, . \]
Model selection
Maximize \[ \hat \ell - \mathop{\mathrm{tr}}(\hat J^{-1} \hat K) \] over the set of candidate models.
Minimize \[ -2 \hat\ell\ + 2\mathop{\mathrm{tr}}(\hat J^{-1}\hat K) \tag{3}\] over the set of candidate models.
(3) is called the Takeuchi Information Criterion (TIC)1 and has also been refereed to as the Network Information Criterion2.
Akaike information criterion
If \(g(\theta) = f(y \,;\,\theta_0)\), then \(\theta_0 = \theta_g\), \(K(\theta_g) = I(\theta_g)\), and, hence,
\[ {\mathop{\mathrm{E}}}_g\{\bar \ell(\hat \theta)\} - \Delta \approx \frac{1}{n} \mathop{\mathrm{tr}}\{I(\theta_g)^{-1} K(\theta_g)\} = p / n \]
Model selection
Maximize \[ \hat \ell - p \] over the set of candidate models.
Minimize \[ -2 \hat\ell\ + 2 p \tag{4}\] over the set of candidate models.
(4) is called the Akaike Information Criterion (AIC)1.
Variable selection with the normal linear model
Data
\(n\)-vector of responses \(y = (y_1, \ldots, y_n)^\top\)
\(n \times p_*\) matrix \(X_*\) with \(j\)th column \(v_j\), \(j \in \mathcal{I}= \{1, \ldots, p_*\}\)
True relationship between \(y\) and \(X\)
\(Y = \mu + \epsilon\), \(\epsilon \sim {\mathop{\mathrm{N}}}_p (0, I_n \sigma^2)\), \(I_n\) the \(n \times n\) identity matrix
AIC for normal linear models
Candidate model
\(Y = X\beta + \epsilon\), \(\epsilon \sim {\mathop{\mathrm{N}}}_p (0, I_n \sigma^2)\)
where \(X\) consists of the columns of \(X_*\) with indices in \(\mathcal{S}\subseteq \mathcal{I}\), \(|\mathcal{S}| = p \le p_*\)
The AIC for the normal linear model takes the form1 \[ {\rm AIC} = n \log\hat\sigma^2 + 2 p + \overbrace{n + n \log(2\pi)}^{\text{can be omitted}} \,, \quad \text{where} \quad \hat\sigma^2 = \frac{Y^\top(I - H)Y}{n} \]
AIC depends only on \(n\), \(p\) (the number of regression parameters in the candidate model), and the ML estimator of the error variance \(\sigma^2\).
AIC will typically select more and more complex models as the samples size increases, because the first-term grows proportionally with \(n\) while the penalty is proportional to \(p\).
A more refined AIC-like criterion (aka corrected AIC, and denoted as \({\rm AIC}_c\), can be derived by the arguments we used to derive AIC in the specific case of the normal linear model.
Corrected AIC for normal linear models
As before, suppose that model selection is by maximization of \[ n \Delta = {\mathop{\mathrm{E}}}_g\left[ {\mathop{\mathrm{E}}}^+_g\left\{ \ell^+(\hat\beta, \hat\sigma^2) \right\} \right] \tag{5}\]
For the normal linear model1 \[ {\mathop{\mathrm{E}}}^+_g\left\{\ell^+(\hat\beta, \hat\sigma^2) \right\} = - \frac{n}{2} \left[ \log \hat\sigma^2 + \frac{n}{Z_1} + \frac{Z_2}{Z_1} + \log(2 \pi)\right] \tag{6}\] where \(Z_1 = n \hat\sigma^2 / \sigma^2\), and \(Z_2 = \|X \hat\beta - \mu\|_2^2 / \sigma^2\).
Under the assumption that \(X\) results in a correct model (i.e. \(\mu = H \mu\)), \(Z_2 \sim \chi_p^2\) independently of \(Z_1\). Using the fact that an inverse \(\chi^2_v\) with \(v > 2\) has expectation \(1/(v - 2)\), model selection by minimum KL divergence, minimizes \[ -2 n \Delta = n {\mathop{\mathrm{E}}}_g( \log \hat\sigma^2) + \frac{n(n + p)}{n - p - 2} + \overbrace{n \log(2 \pi)}^{\text{can be omitted}} \tag{7}\]
Corrected AIC for normal linear models
So, we can select models by minimizing \[ {\rm AIC}_c = n \log \hat\sigma^2 + n\frac{1 + p / n}{1 - (p + 2) / n} \] over the set of candidate models.
A Taylor expansion of the second term for large \(n\), gives \[ {\rm AIC}_c = \overbrace{n \log \hat\sigma^2 + 2 p}^{{\rm AIC}} + 2 + O(p^2 / n) \] and so \({\rm AIC}_c\) and \({\rm AIC}\) will tend to select the same model.
When \(p\) is comparable to \(n\), \({\rm AIC}_c\) penalizes model complexity more severely.
Model selection criteria
| Definition | Key assumptions | Target | |
|---|---|---|---|
| AIC | \(-2\hat\ell + 2p\) | ML estimation; \(g(y) = f(y \,;\,\theta_0)\) | min KL divergence |
| TIC | \(-2\hat\ell\ + 2\mathop{\mathrm{tr}}(\hat J^{-1}\hat K)\) | ML estimation | min KL divergence |
| AIC\(_c\) | \(-2\hat\ell + n(n-p)/(n - p - 2)\) | ML estimation; \(g(y) = f(y \,;\,\theta_0)\); normal linear model | min KL divergence |
\(p\) is the number of parameters in a candidate model and \(\hat\ell\) the corresponding maximized log-likelihood.
BIC
Bayesian inference
Frequentist viewpoint (cartoon version)
There is a quantity \(\theta\) that characterizes aspects of how the data is generated and is treated as an unknown constant.
Probability statements concern randomness in hypothetical replications of the data (possibly conditioned on an ancillary statistic).
Bayesian viewpoint (cartoon version)
All ignorance should be expressed in terms of probability statements.
A joint probability distribution for data and all unknowns can be constructed.
Bayes’ theorem is used to convert prior beliefs \(\pi(\theta)\) about unknown \(\theta\) into posterior beliefs \(\pi(\theta\mid y)\), conditioned on data.
Probability statements concern randomness of unknowns, conditioned on all known quantities.

A joke by Xiao-Li Meng
Bayesian updating
| Quantity | Captures | |
|---|---|---|
| Data | \(y\) | reality |
| Likelihood | \(f(y \mid \theta)\), \(\theta\in\Omega_\theta\) | modelling assumptions / experimental conditions |
| Prior distribution | \(\pi(\theta)\) | prior information about \(\theta\) |
| Posterior distribution | \(\displaystyle \pi(\theta\mid y ) = \frac{\pi(\theta) f(y\mid\theta)}{\int \pi(\theta) f(y\mid\theta)\, d\theta}\) | information about \(\theta\), conditional on the observed data \(y\) |
Marginal posterior
If \(\theta = (\psi^\top,\lambda^\top)^\top\), then inference for \(\psi\) is based on the marginal posterior \[ \pi(\psi\mid y) = \int \pi(\theta\mid y )\, d\lambda \]
Bayesian model selection
A set of \(M\) candidate models, with respective parameters \(\theta_1 \in \Omega_{1}, \ldots, \theta_M \in \Omega_{M}\)
| Quantity | |
|---|---|
| Parameter space | \(\theta \in \Omega = \bigcup_{m=1}^M \{m\}\times \Omega_{m}\) |
| Prior distributions for parameters of model \(m\) | \(\pi(\theta_m \mid m)\) |
| Prior probabilities for models | \(\pi(m)\) |
| Likelihood of model \(m\) | \(f(y \mid \theta_m, m)\) |
Inference about model choice
Marginal posterior probability mass function
\[ \pi(m\mid y) = \frac{\int_{\Omega_m} f(y \mid \theta_m, m) \pi(\theta_m \mid m) \pi(m)\, d\theta_m} {\sum_{m'=1}^M \int_{\Omega_{m'}} f(y \mid \theta_{m'}, m') \pi(\theta_{m'} \mid m') \pi(m')\, d\theta_{m'}} = \frac{\pi(m)}{f(y)} \rho_m(y) \] where \(\rho_{m'}(y)\) is the marginal likelihood, and \(f(y) = \sum_{m'=1}^M \pi(m') \rho_{m'}(y)\) is not important for model comparison since it is constant in the set of candidate models.
Marginal likelihood
\[ \rho_m(y) = \int_{\Omega_m} f(y \mid \theta_m, m) \pi(\theta_m \mid m)\, d\theta_m \]
- Not available in closed form for general models, and may be difficult/intensive to compute
- Requires specification of priors for the parameters of each model
Bayesian updating
\[ \pi(\theta_m\mid m)\pi(m) \mapsto \pi(\theta_m \mid m, y) \pi(m\mid y) \]
For each model \(m \in \{1,\ldots, M\}\), it is necessary to compute
\(\pi(m \mid y)\), which involves \(\rho_m(y) = \int f(y\mid\theta_m,m)\pi(\theta_m\mid m)\, d\theta_m\)
\(\pi(\theta_m \mid y, m)\)
Posterior odds = Prior odds \(\times\) Bayes factor
If there are just two models, we can write \[ \underbrace{\frac{\pi(1\mid y)}{\pi(2\mid y)}}_{\text{Posterior odds}} = \overbrace{\frac{\pi(1)}{\pi(2)}}^{\text{Prior odds}} \underbrace{\frac{\rho_1(y)}{\rho_2(y)}}_{\text{Bayes factor}} \]
Lindsey’s paradox
Suppose that \(\theta_m\) has as \(N(0, \sigma^2 I_{p_m})\) prior, where \(\sigma^2\) is large (prior is diffuse). Then, \[ \begin{aligned} f(y \mid m) &= \sigma^{-p_m} (2\pi)^{-p_m/2} \int f(y \mid m, \theta_m) \prod_{r = 1}^{p_m} \exp \left\{-{\theta_{m,r}^2/(2\sigma^2)}\right\} d\theta_{m, r}\\ & \approx \sigma^{-p_m} (2\pi)^{-p_m/2} \int f(y \mid m, \theta_m) \prod_{r = 1}^{p_m} d\theta_{m, r} \end{aligned} \]
The Bayes factor for comparing two models is \[ \frac{\rho_1(y)}{\rho_2(y)} \approx \sigma^{p_2 - p_1} g(y) \] where \(g(y)\) depends on the two likelihoods but is independent of \(\sigma^2\).
\[\LARGE\Downarrow\]
Irrespective of what the data tell us about the relative merits of the two models, the Bayes factor in favour of the simpler model can be made arbitrarily large by increasing \(\sigma\).
Model averaging
If a quantity \(Z\) has the same interpretation for all models, it is desirable to allow for model uncertainty when constructing inferences or making predictions about it.
Predictive distribution of \(Z\)
\[ f(z\mid y) = \sum_{m=1}^M f(z\mid m, y) \pi(m \mid y) \]
\(Z\) is a future value
Each model may be just a vehicle that provides a future value, and not of interest on its own.
\(Z\) is a physical parameter (e.g. means, variances, etc.)
Care is needed with prior choice and ensuring that \(Z\) has the same interpretation across models.
Towards a Bayesian information criterion
Suppose that \(y = (y_1, \ldots, y_n)^\top\)1, and that \[ f_m(y_1, \ldots, y_n \mid \theta_m, m) = \prod_{i = 1}^n f_m(y_i \mid \theta_m, m) \]
Let \[ {\rm BIC}^{\rm exact}_m = - 2 \log \rho_m(y) \]
Then,
\[ \pi(m \mid y) = \frac{\pi(m) \exp\left\{-\frac{1}{2} {\rm BIC}^{\rm exact}_m\right\}}{\sum_{m' = 1}^M \pi(m') \exp\left\{-\frac{1}{2} {\rm BIC}^{\rm exact}_{m'}\right\}} \]
If all models in the candidate set of models are equally likely (\(\pi(1) = \ldots = \pi(M)\)), then the model with the smallest \({\rm BIC}^{\rm exact}_m\) value has the highest posterior probability.
Laplace approximation
Suppose that \(h(z)\) and \(\pi(z)\) are twice continuously differentiable real functions in a subset of \(\mathcal{Z} \subset \Re^p\), that \(z_0 = \arg \max_{z \in \mathcal{Z}} h(z)\) is unique, and that \(\pi(z) = O(1)\) and \(\pi(z_0) \ne 0\). Then,
\[ \int_\mathcal{Z} \exp\{n h(z)\} \pi(z)\, d z = \left(\frac{2\pi}{n} \right)^{p/2} \exp\left\{n h(z_0) \right\} \left\{\pi(z_0) | G(z_0)|^{-1/2} + O(n^{-1}) \right\} \tag{8}\] where \(G(z) = - \nabla \nabla^\top h(z)\).
Towards a Bayesian information criterion
Replacing \(h(z)\) by \(n^{-1} \ell_m(\theta) = n^{-1} \log f(y \mid \theta_m, m)\) and \(\pi(z)\) by \(\pi(\theta_m \mid m)\) in (8) gives
\[ \rho_m(y) \simeq \exp\{\ell_m(\hat\theta_m)\} (2\pi)^{p_m/2} n^{-p_m/2} |n^{-1} J_m(\hat\theta_m)|^{-1/2} \pi(\hat\theta_m \mid m) \] where \(J_m(\theta_m) = -\nabla \nabla^\top \ell_m(\theta_m)\)1.
Then, \[ {\rm BIC}^{\rm exact}_m \approx \overbrace{-2 \ell_m(\hat\theta_m)}^{O_p(n)} + \underbrace{p_m \log n}_{O(\log n)} - \overbrace{p_m \log (2\pi) + \log |n^{-1} J_m(\hat\theta_m)| + \log \pi(\hat\theta_m \mid m)}^{O(1)} \]
Bayesian information criterion
So large sample approximations to \({\rm BIC}^{\rm exact}_m\) and \(\pi(m \mid y)\) are \[ {\rm BIC}_m = -2 \ell_m(\hat\theta_m) + p_m \log n \quad \text{and} \quad \pi(m \mid y) = \frac{\pi(m) \exp\left\{-\frac{1}{2} {\rm BIC}_m\right\}}{\sum_{m' = 1}^M \pi(m') \exp\left\{-\frac{1}{2} {\rm BIC}_{m'}\right\}} \]
The priors \(\pi(\theta_m \mid m)\) do not appear in the above expressions.1
Model selection
If all models in the candidate set of models are equally likely
Maximize \[ \hat \ell - p \log n / 2 \] over the set of candidate models.
Minimize \[ -2 \hat\ell\ + p \log n \tag{9}\] over the set of candidate models.
Model selection criteria
| Definition | Key assumptions | Target | |
|---|---|---|---|
| AIC | \(-2\hat\ell + 2p\) | ML estimation; \(g(y) = f(y \,;\,\theta_0)\) | min KL divergence |
| TIC | \(-2\hat\ell\ + 2\mathop{\mathrm{tr}}(\hat J^{-1}\hat K)\) | ML estimation | min KL divergence |
| AIC\(_c\) | \(-2\hat\ell + n(n-p)/(n - p - 2)\) | ML estimation; \(g(y) = f(y \,;\,\theta_0)\); normal linear model | min KL divergence |
| BIC | \(-2\hat\ell\ + p\log n\) | ML estimation; \(\pi(1) = \ldots = \pi(m)\) | max \(\pi(m \mid y)\) |
\(p\) is the number of parameters in a candidate model and \(\hat\ell\) the corresponding maximized log-likelihood.
Nodal involvement: AIC
Considering only the models with an intercept and without any interaction between the 5 binary covariates, results in \(2^5 = 32\) possible logistic regression models for this data.
Global model call: glm(formula = r ~ aged + stage + grade + xray + acid, family = "binomial",
data = nodal, na.action = "na.fail")
---
Model selection table
(Intrc) acid aged grade stage xray df logLik AIC delta weight
26 -3.0520 + + + 4 -24.590 57.2 0.00 0.225
30 -3.2620 + + + + 5 -23.880 57.8 0.58 0.169
28 -2.7780 + + + + 5 -24.380 58.8 1.58 0.102
22 -2.7340 + + + 4 -25.409 58.8 1.64 0.099
32 -3.0790 + + + + + 6 -23.805 59.6 2.43 0.067
25 -2.0820 + + 3 -27.231 60.5 3.28 0.044
18 -2.1760 + + 3 -27.394 60.8 3.61 0.037
24 -2.6870 + + + + 5 -25.404 60.8 3.63 0.037
14 -2.8940 + + + 4 -26.581 61.2 3.98 0.031
27 -1.7350 + + + 4 -26.606 61.2 4.03 0.030
29 -2.1960 + + + 4 -26.763 61.5 4.35 0.026
10 -2.5090 + + 3 -27.957 61.9 4.73 0.021
6 -2.4180 + + 3 -28.131 62.3 5.08 0.018
20 -1.9750 + + + 4 -27.230 62.5 5.28 0.016
31 -1.8760 + + + + 5 -26.330 62.7 5.48 0.015
16 -2.6770 + + + + 5 -26.461 62.9 5.74 0.013
12 -2.1860 + + + 4 -27.542 63.1 5.90 0.012
21 -1.6030 + + 3 -28.724 63.4 6.27 0.010
8 -2.3550 + + + 4 -28.122 64.2 7.06 0.007
17 -1.1350 + 2 -30.465 64.9 7.75 0.005
23 -1.3830 + + + 4 -28.523 65.0 7.87 0.004
19 -0.8648 + + 3 -30.013 66.0 8.85 0.003
11 -1.1090 + + 3 -30.222 66.4 9.26 0.002
13 -1.6550 + + 3 -30.270 66.5 9.36 0.002
9 -1.4350 + 2 -31.276 66.6 9.37 0.002
2 -1.5580 + 2 -31.355 66.7 9.53 0.002
15 -1.3330 + + + 4 -29.648 67.3 10.12 0.001
4 -1.3240 + + 3 -31.106 68.2 11.03 0.001
5 -1.0990 + 2 -32.336 68.7 11.49 0.001
7 -0.8611 + + 3 -32.040 70.1 12.90 0.000
1 -0.5008 1 -35.126 72.3 15.07 0.000
3 -0.2076 + 2 -34.433 72.9 15.69 0.000
Models ranked by AIC(x) Nodal involvement: BIC
Considering only the models with an intercept and without any interaction between the 5 binary covariates, results in \(2^5 = 32\) possible logistic regression models for this data.
Global model call: glm(formula = r ~ aged + stage + grade + xray + acid, family = "binomial",
data = nodal, na.action = "na.fail")
---
Model selection table
(Intrc) acid aged grade stage xray df logLik BIC delta weight
26 -3.0520 + + + 4 -24.590 65.1 0.00 0.220
25 -2.0820 + + 3 -27.231 66.4 1.31 0.114
22 -2.7340 + + + 4 -25.409 66.7 1.64 0.097
18 -2.1760 + + 3 -27.394 66.7 1.64 0.097
30 -3.2620 + + + + 5 -23.880 67.6 2.55 0.061
10 -2.5090 + + 3 -27.957 67.8 2.76 0.055
6 -2.4180 + + 3 -28.131 68.2 3.11 0.046
28 -2.7780 + + + + 5 -24.380 68.6 3.55 0.037
17 -1.1350 + 2 -30.465 68.9 3.81 0.033
14 -2.8940 + + + 4 -26.581 69.0 3.98 0.030
27 -1.7350 + + + 4 -26.606 69.1 4.03 0.029
21 -1.6030 + + 3 -28.724 69.4 4.30 0.026
29 -2.1960 + + + 4 -26.763 69.4 4.35 0.025
20 -1.9750 + + + 4 -27.230 70.3 5.28 0.016
9 -1.4350 + 2 -31.276 70.5 5.43 0.015
2 -1.5580 + 2 -31.355 70.6 5.59 0.013
24 -2.6870 + + + + 5 -25.404 70.7 5.60 0.013
12 -2.1860 + + + 4 -27.542 71.0 5.90 0.011
32 -3.0790 + + + + + 6 -23.805 71.4 6.37 0.009
19 -0.8648 + + 3 -30.013 71.9 6.88 0.007
8 -2.3550 + + + 4 -28.122 72.1 7.06 0.006
11 -1.1090 + + 3 -30.222 72.4 7.29 0.006
13 -1.6550 + + 3 -30.270 72.5 7.39 0.005
31 -1.8760 + + + + 5 -26.330 72.5 7.45 0.005
5 -1.0990 + 2 -32.336 72.6 7.55 0.005
16 -2.6770 + + + + 5 -26.461 72.8 7.71 0.005
23 -1.3830 + + + 4 -28.523 72.9 7.87 0.004
4 -1.3240 + + 3 -31.106 74.1 9.06 0.002
1 -0.5008 1 -35.126 74.2 9.16 0.002
15 -1.3330 + + + 4 -29.648 75.2 10.12 0.001
7 -0.8611 + + 3 -32.040 76.0 10.93 0.001
3 -0.2076 + 2 -34.433 76.8 11.75 0.001
Models ranked by BIC(x) Nodal involvement: AIC, BIC
R code
par(mfrow = c(1, 2))
plot(AIC ~ df, data = mods_AIC, xlab = "Number of parameters",
bg = "#ff7518", pch = 21)
points(AIC ~ df, data = mods_AIC |> aggregate(AIC ~ df, min), type = "l")
plot(BIC ~ df, data = mods_BIC, xlab = "Number of parameters",
bg = "#ff7518", pch = 21)
points(BIC ~ df, data = mods_BIC |> aggregate(BIC ~ df, min), type = "l")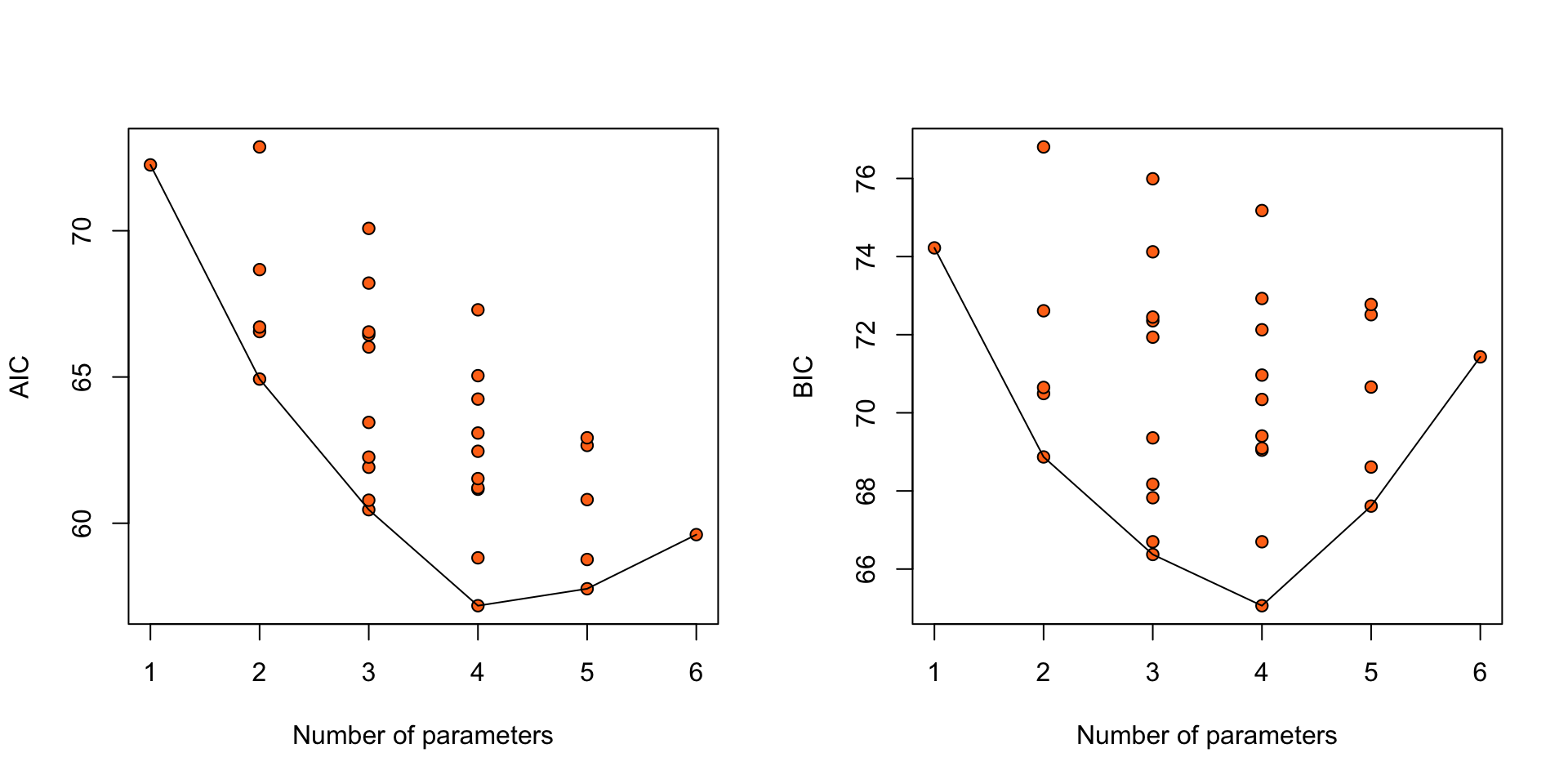
Figure 12: AIC and BIC for 32 logistic regression models for the nodal data.
Simulation study: Linear regression
R code
get_X <- function(n, p) {
X <- matrix(rnorm(n * p), nrow = n)
scale(X, center = TRUE, scale = TRUE)
}
get_y <- function(R, X, beta, sigma = 1) {
eta <- drop(X %*% beta)
## Simulate R error vectors of length $n$
epsilon <- matrix(rnorm(R * nrow(X), 0, sigma), ncol = R)
eta + epsilon
}
get_logliks <- function(y, X) {
sapply(1:ncol(X), function(j) logLik(lm(y ~ -1 + X[, 1:j])))
}
selection_frequencies <- function(R, n, beta, sigma = 1) {
p <- length(beta)
X <- get_X(n, p)
ys <- get_y(R, X, beta, sigma = sigma)
ps <- 1:p
lls <- apply(ys, 2, \(y) get_logliks(y, X))
AICs <- -2 * lls + 2 * ps
AICcs <- -2 * lls + (n * (n + ps)) / (n - ps - 2)
BICs <- -2 * lls + ps * log(n)
sel_AIC <- table(apply(AICs, 2, which.min))
sel_AICc <- table(apply(AICcs, 2, which.min))
sel_BIC <- table(apply(BICs, 2, which.min))
out <- data.frame(freq = c(sel_AIC, sel_AICc, sel_BIC),
IC = c(rep("AIC", length(sel_AIC)),
rep("AICc", length(sel_AICc)),
rep("BIC", length(sel_BIC))),
model = c(names(sel_AIC), names(sel_AICc), names(sel_BIC)),
n = n,
R = R)
out$model <- factor(out$model, levels = ps, ordered = TRUE)
out
}Model matrix
- Simulate \(np\) independent \(N(0, 1)\)
- Organize them into an \(n \times p\) matrix
- Centre and scale the columns so that each column has mean \(0\) and variance \(1\).
Response vector
- Simulate \(R\) response vectors as \(Y = X\beta + \epsilon\), \(\epsilon \sim \mathop{\mathrm{N}}(0, \sigma^2 I_n)\)
Information criteria
- For each response vector, fit linear models using: column 1 of \(X\), column 1, 2 of \(X\), column 1, 2, 3 of \(X\), and so on.
- For each fit compute AIC, AIC\(_c\), BIC, and count the frequency each of the \(p\) models is selected.
Simulation study: Linear regression
\(\beta = (3, 2, 1, 1, 1, 1, 0)^\top\), \(\sigma = 1\)
R code
ns <- c(10, 20, 40, 80, 160, 320, 640)
set.seed(123)
sel_probs <- lapply(ns, function(n) selection_frequencies(1000, n, c(3, 2, 1, 1, 1, 1, 0)))
sel_probs <- do.call("rbind", sel_probs)
ggplot(sel_probs) +
geom_col(aes(x = model, y = freq, color = IC, fill = IC), position = "dodge") +
facet_grid(IC ~ n, labeller = label_both) +
theme_minimal() +
labs(x = "# of covariates", y = "Selection frequency")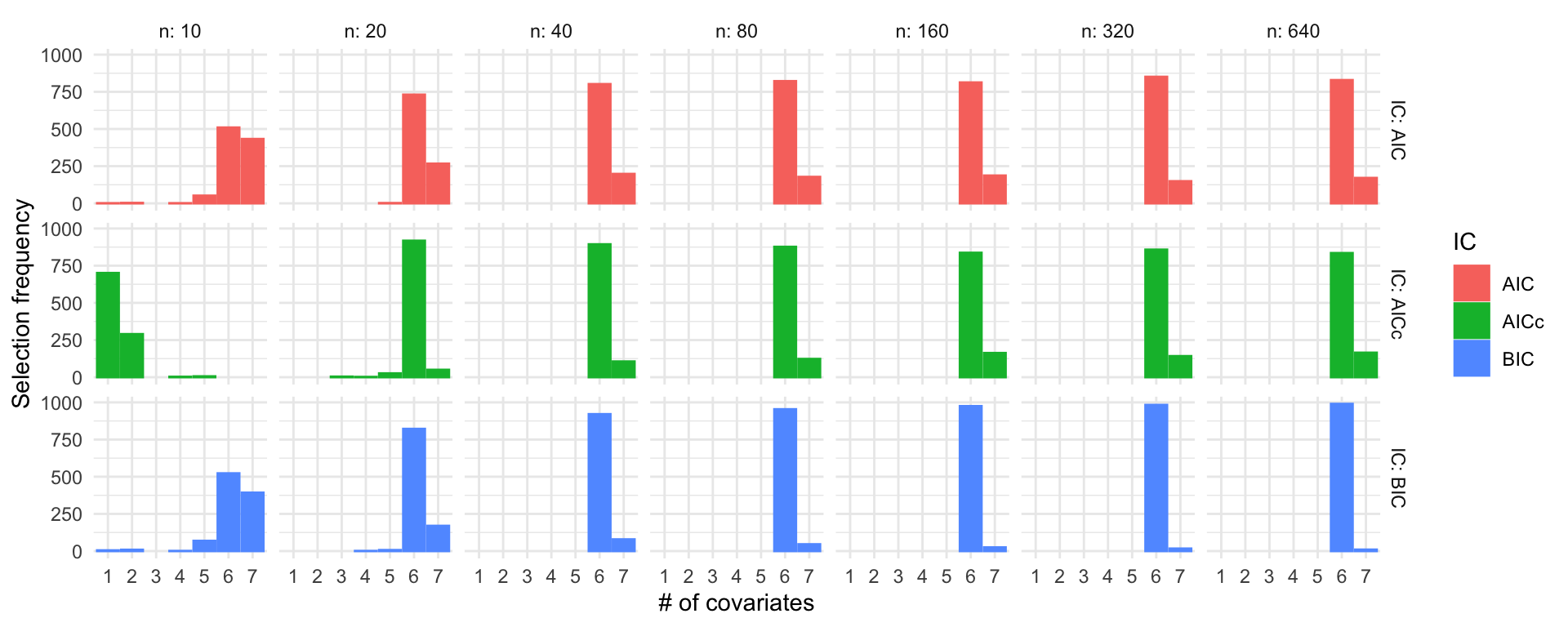
Simulation study: Linear regression
\(\beta = (3, 2, 1, 0, 0, 0, 0)^\top\), \(\sigma = 1\)
R code
ns <- c(10, 20, 40, 80, 160, 320, 640)
set.seed(123)
sel_probs <- lapply(ns, function(n) selection_frequencies(1000, n, c(3, 2, 1, 0, 0, 0, 0)))
sel_probs <- do.call("rbind", sel_probs)
ggplot(sel_probs) +
geom_col(aes(x = model, y = freq, color = IC, fill = IC), position = "dodge") +
facet_grid(IC ~ n, labeller = label_both) +
theme_minimal() +
labs(x = "# of covariates", y = "Selection frequency")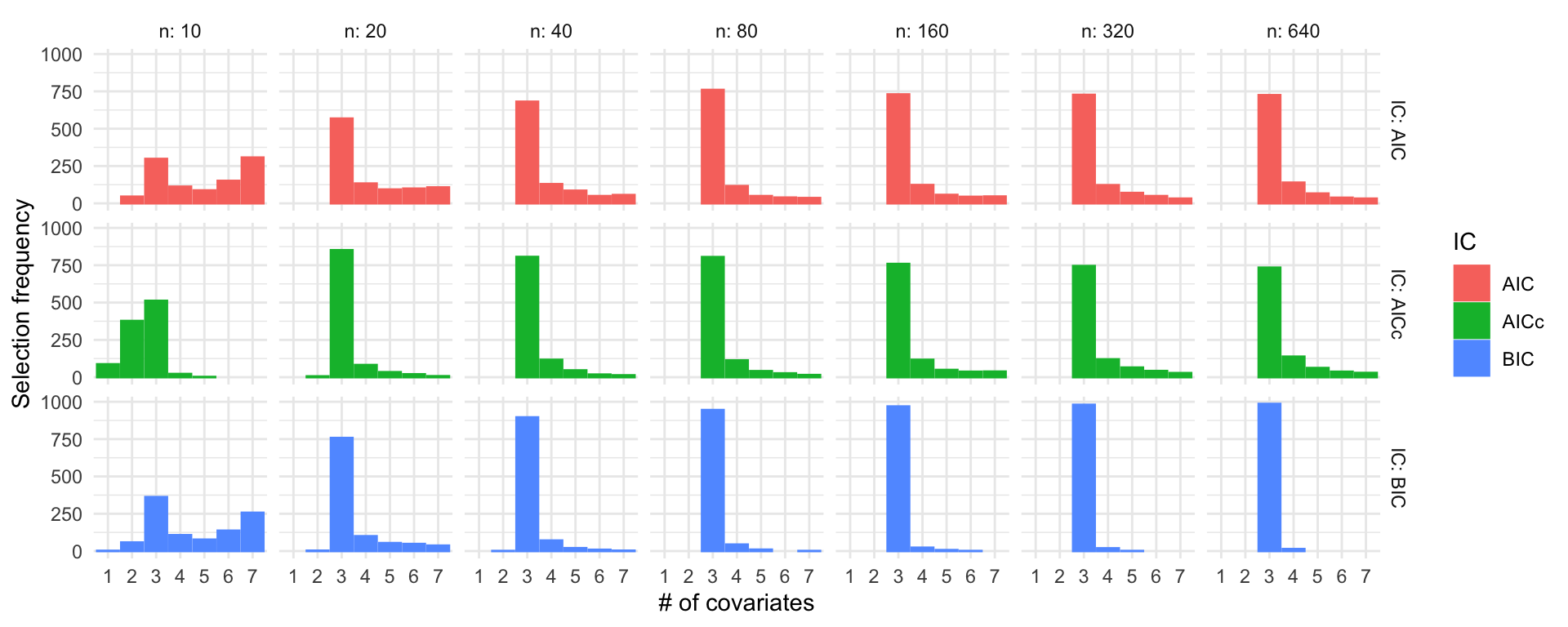
Simulation study: Linear regression
\(\beta = (3, 0, 0, 0, 0, 0, 0)^\top\), \(\sigma = 1\)
R code
ns <- c(10, 20, 40, 80, 160, 320, 640)
set.seed(123)
sel_probs <- lapply(ns, function(n) selection_frequencies(1000, n, c(3, 0, 0, 0, 0, 0, 0)))
sel_probs <- do.call("rbind", sel_probs)
ggplot(sel_probs) +
geom_col(aes(x = model, y = freq, color = IC, fill = IC), position = "dodge") +
facet_grid(IC ~ n, labeller = label_both) +
theme_minimal() +
labs(x = "# of covariates", y = "Selection frequency")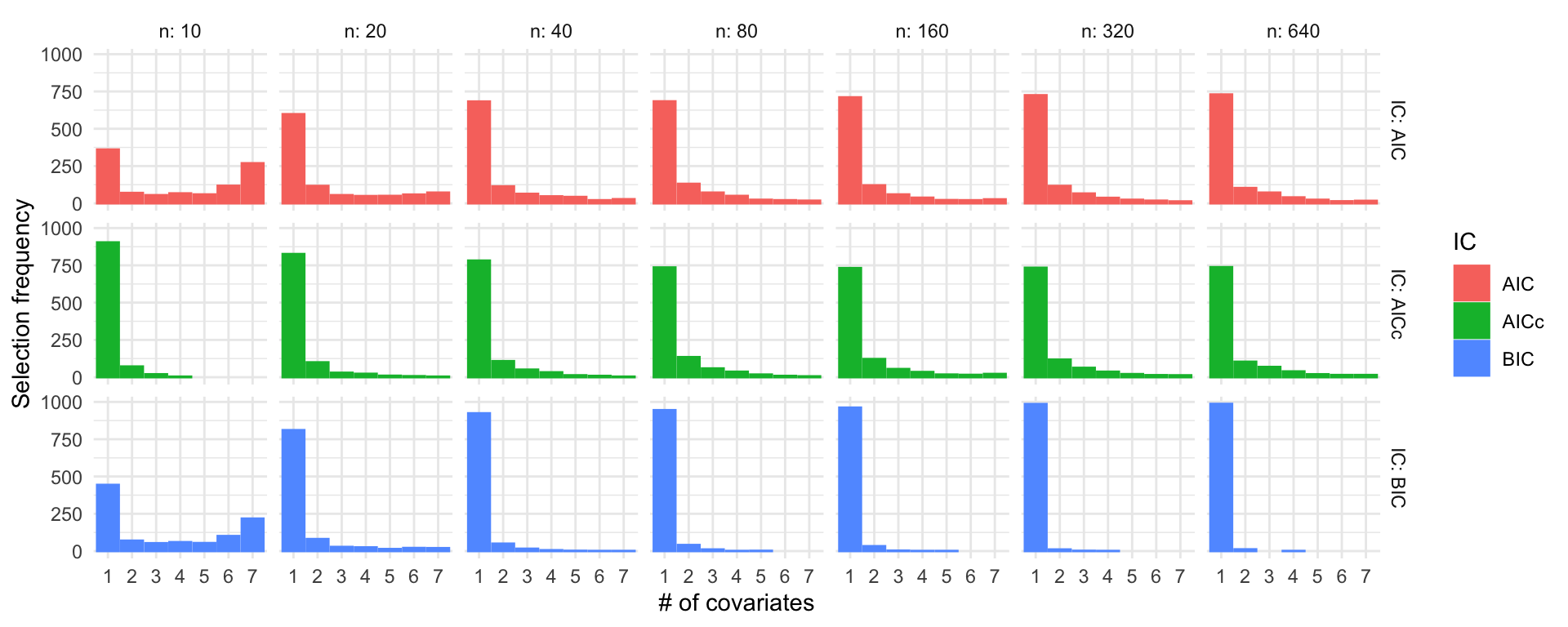
Simulation study: Linear regression
\(\beta = (3, 2, 1, 0, 0, 0, 0)^\top\), \(\sigma = 1\)
R code
ns <- c(10, 20, 40, 80, 160, 320, 640)
set.seed(123)
sel_probs <- lapply(ns, function(n) selection_frequencies(1000, n, c(3, 2, 1, 0, 0, 0, 0)))
sel_probs <- do.call("rbind", sel_probs)
ggplot(sel_probs) +
geom_col(aes(x = model, y = freq, color = IC, fill = IC), position = "dodge") +
facet_grid(IC ~ n, labeller = label_both) +
theme_minimal() +
labs(x = "# of covariates", y = "Selection frequency")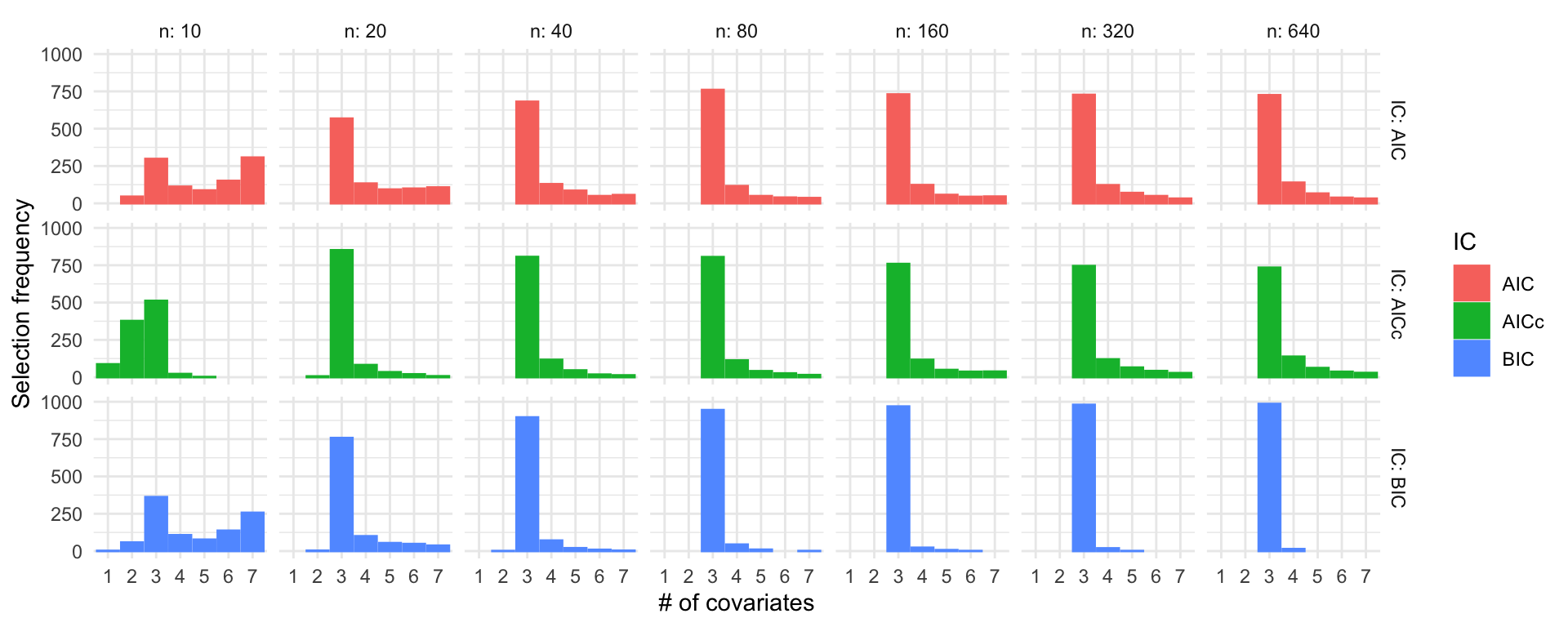
Simulation study: Linear regression
\(\beta = (3, 2, 1, 0, 0, 0, 0)^\top\), \(\sigma = 3\)
R code
ns <- c(10, 20, 40, 80, 160, 320, 640)
set.seed(123)
sel_probs <- lapply(ns, function(n) selection_frequencies(1000, n, c(3, 2, 1, 0, 0, 0, 0), sigma = 3))
sel_probs <- do.call("rbind", sel_probs)
ggplot(sel_probs) +
geom_col(aes(x = model, y = freq, color = IC, fill = IC), position = "dodge") +
facet_grid(IC ~ n, labeller = label_both) +
theme_minimal() +
labs(x = "# of covariates", y = "Selection frequency")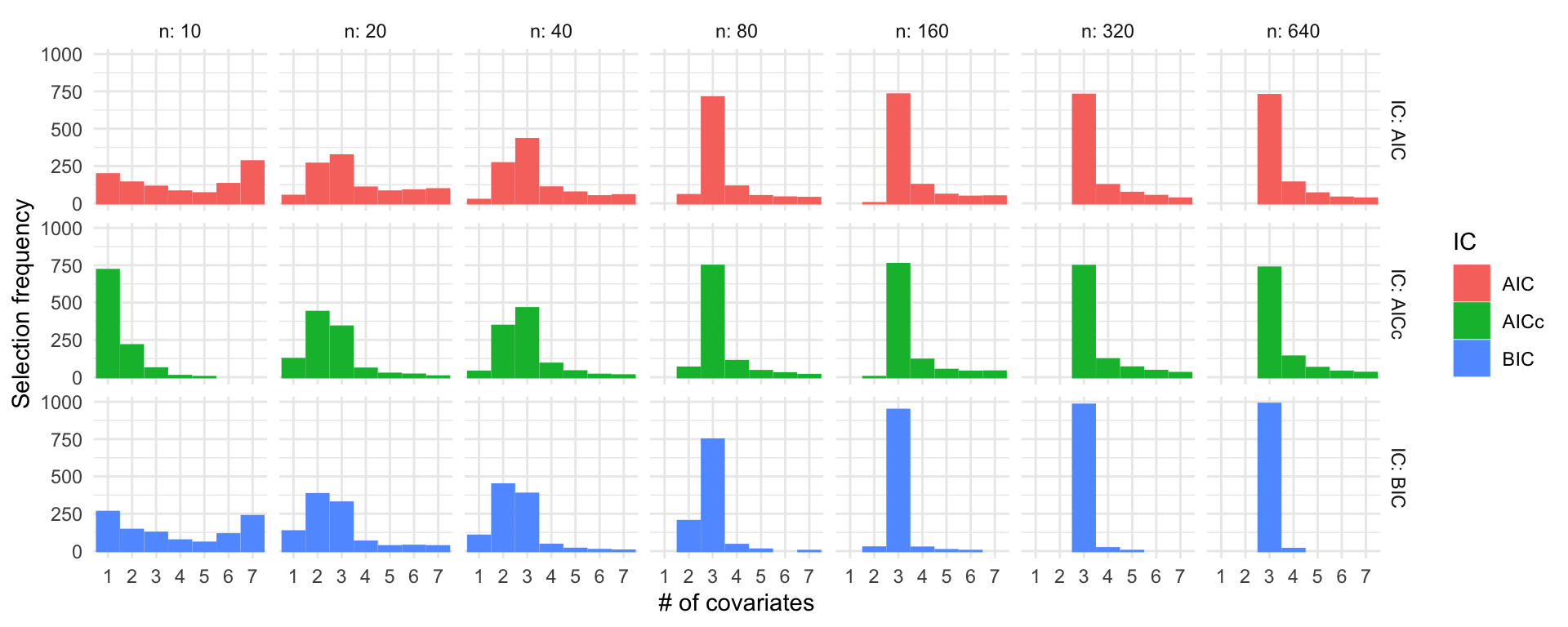
Consistency and asymptotic efficiency
Properties of model selection procedures1
Consistency
Suppose that the true model is among the candidate models. A model selection procedure that selects the true model with probability tending to one as \(n\to\infty\) is called consistent.
Asymptotic efficiency
A model selection procedure that selects the candidate “closest” to the true model for large \(n\) is called asymptotically efficient.
Asymptotic analysis of AIC, BIC, TIC
Let \(\text{IC} = - 2\hat\ell + c(n, p)\) be an information criterion for a correct model, and IC\(_+\) be the value of the information criterion for an encompassing model with one extra parameter.
\[ \begin{aligned} P(\text{IC}_+ < \text{IC}) &= P\left\{ c(n,p+1)-2\hat\ell_+< c(n,p)-2\hat\ell\right\} \\ & = P\left\{2(\hat\ell_+ - \hat\ell) > d(n, p) \right\} \end{aligned} \]
| Criterion | \(d(n, p)\) |
|---|---|
| AIC | \(= 2\) |
| TIC | \(\approx 2\) for large \(n\) |
| BIC | \(= \log n\) |
\(2(\hat\ell_+-\hat\ell)\) converges in distribution to a \(\chi^2_1\) random variable. So, as \(n\to\infty\), \[ P(\text{IC}_+<\text{IC}) \to \begin{cases} 0.157, & \text{if AIC or TIC is used} \\ 0, & \text{if BIC is used} \end{cases} \]
Is there a sweet spot in consistency and efficiency realms?
Unfortunately, there is not…
Yang (2005) shows that
For any model selection criterion to be consistent, it must behave sub-optimally for estimating the regression function in terms of minimax rate of convergence1
Direct estimates of generalization error
Data-splitting
An alternative to information criteria is to use data-splitting principles to attempt and directly estimate a measure of generalization error, typically under less assumptions about the data generating process than what is required for the asymptotic validity of information criteria.
Expected prediction error in linear regression
For example, one approach to select across candidate linear regression models is to minimize the expected prediction error \[ \Delta = n^{-1} {\mathop{\mathrm{E}}} \left[{\mathop{\mathrm{E}}}^+\left\{ \|Y^+ - X\hat\beta\|_2^2 \right\}\right] = \underbrace{\mu^\top (I_n - H) \mu / n}_{\text{Bias}^2} + \overbrace{(1 + p / n) \sigma^2}^{\text{Variance}} \] across the set of candidates models, where \(Y^+ = \mu + \epsilon^{+}\), with \(\epsilon^+\) an independent copy of \(\epsilon\), and expectation \({\mathop{\mathrm{E}}}(\cdot)\) is with respect to \(Y\) and \({\mathop{\mathrm{E}}}^+(\cdot)\) with respect to \(Y^+\).1
\(\Delta\) depends on \(\mu\) and \(\sigma^2\), which are unknown.
Information criteria like AIC and TIC, typically result by considering asymptotically unbiased estimators of \(\Delta\), and information criteria like BIC result by assuming overwhelming information about the candidate models relative to the prior information about the parameters.
Validation set approach: linear models
We can use the assumption of exchangeability of \(Y_1, \ldots, Y_n\) conditional on \(X\) to estimate \(\Delta\).
For each candidate model:
Split data into a training set \((X, y)\) and a validation set \((X^{+}, y^{+})\), where \(X^{+}\) is an \(n^{+} \times p\) matrix, and \(y^{+}\) is the vector of the corresponding \(n^{+}\) response values.
Estimate the model using \((X, y)\).
Compute the unbiased estimator of \(\Delta\) \[ \hat\Delta = \frac{1}{n^{+}}(y^{+} - X^{+}\hat\beta)^\top (y^{+} - X^{+}\hat\beta) \] where \(\hat\beta\) is the least squares estimator of the candidate model.
Choose the candidate model with the smallest \(\hat\Delta\).
Validation set approach
The choice of generalization error depends on the task at hand and the candidate models.
e.g.
for prediction we may want to focus on mean squared error of predictions;
for classification tasks we may want to focus on misclassification rates;
\(\ldots\)
Depending on \(n\), data splitting may not the most efficient use of the available information.
Cars: ISLR2::Auto
Gas mileage, horsepower, and other information for 392 vehicles.
Rows: 392
Columns: 9
$ mpg <dbl> 18, 15, 18, 16, 17, 15, 14, 14, 14, 15, 15, 14, 15, 14, 2…
$ cylinders <int> 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 4, 6, 6, 6, 4, …
$ displacement <dbl> 307, 350, 318, 304, 302, 429, 454, 440, 455, 390, 383, 34…
$ horsepower <int> 130, 165, 150, 150, 140, 198, 220, 215, 225, 190, 170, 16…
$ weight <int> 3504, 3693, 3436, 3433, 3449, 4341, 4354, 4312, 4425, 385…
$ acceleration <dbl> 12.0, 11.5, 11.0, 12.0, 10.5, 10.0, 9.0, 8.5, 10.0, 8.5, …
$ year <int> 70, 70, 70, 70, 70, 70, 70, 70, 70, 70, 70, 70, 70, 70, 7…
$ origin <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 1, 3, …
$ name <fct> chevrolet chevelle malibu, buick skylark 320, plymouth sa…mpg cylinders displacement horsepower weight acceleration year origin name
mpg ~ horsepower
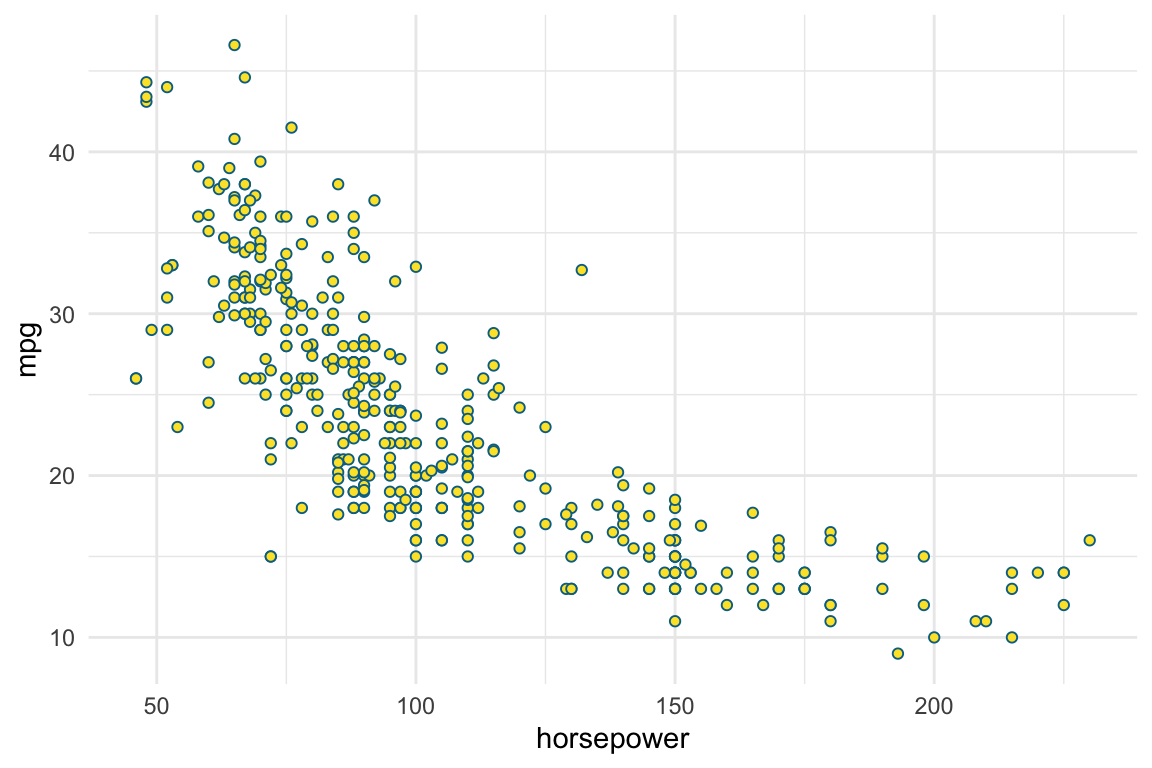
log(mpg) ~ log(horsepower)
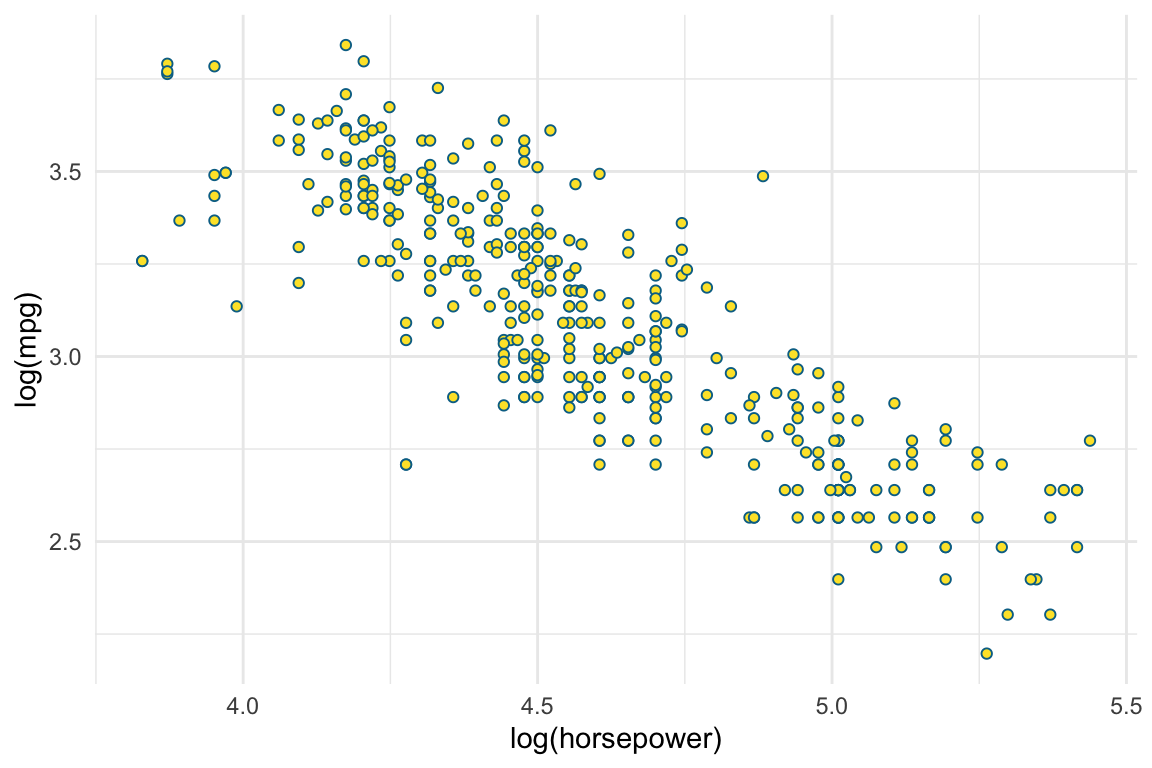
Best \(m\) for mpg ~ poly(horsepower, m)
The following code chunk estimates:
AIC for \(m \in \{1, \ldots, 10\}\),
MSE for \(m \in \{1, \ldots, 10\}\) using \(5\) different random splits of the data into training and validation set
R code
## AIC
degrees <- 1:10
mods <- lapply(degrees, function(degree) lm(mpg ~ poly(horsepower, degree = degree), data = Auto))
AICs <- sapply(mods, AIC)
## Validation sets
set.seed(111)
n_splits <- 5
inds <- replicate(n_splits, sample(1:nrow(Auto), ceiling(nrow(Auto) / 2), replace = FALSE))
MSEv <- sapply(1:n_splits, function(j) {
sapply(degrees, function(degree) {
m <- lm(mpg ~ poly(horsepower, degree = degree), data = Auto, subset = inds[, j])
validation_df <- Auto[-inds[, j], ]
mean((validation_df$mpg - predict(m, newdata = validation_df))^2)
})
})
crits <- data.frame(degree = degrees,
criterion = rep(c(paste0("MSE[split ", 1:n_splits, "]"), "AIC"),
each = length(degrees)),
approach = rep(c("Validation set", "IC"),
c(n_splits * length(degrees), length(degrees))),
value = c(c(MSEv), AICs), check.names = FALSE)
crits <- crits |> group_by(criterion) |> mutate(value = value / min(value))Best \(m\) for mpg ~ poly(horsepower, m)
R code
cols0 <- hcl.colors(6, palette = "Dynamic")
ggplot(crits,
aes(degree, value, col = criterion)) +
geom_line() + geom_point() +
theme_minimal() +
labs(y = "criterion / min(criterion)") +
lims(y = range(crits$value)) +
scale_x_continuous(breaks = 1:10) +
scale_color_manual(values = cols0) +
facet_wrap(~ approach, scales = "free_y")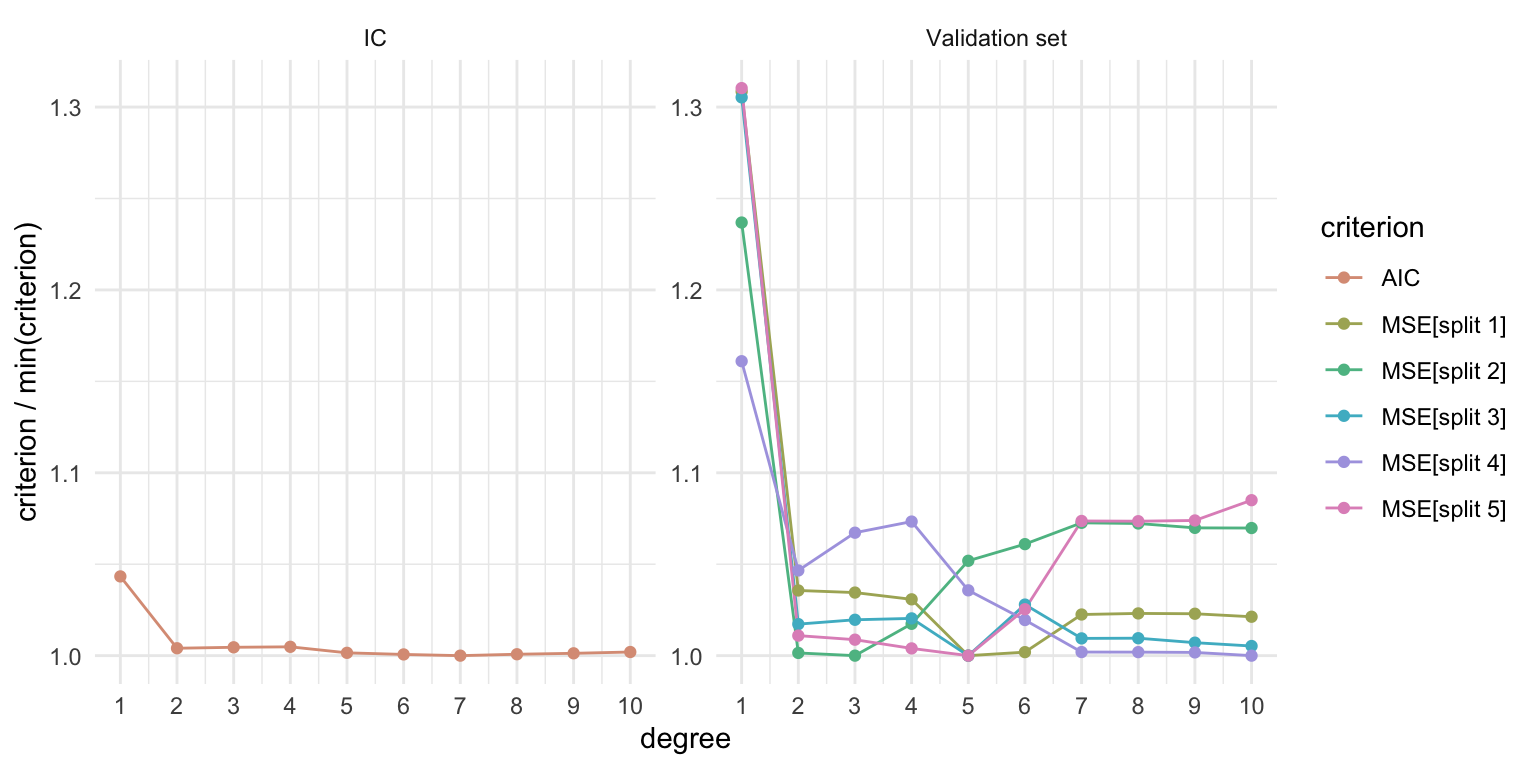
\(k\)-fold cross-validation
Procedure
Randomly split the data into \(k\) non-overlapping groups (folds)
For \(j \in \{1, \ldots, k\}\):
2.1 Use \(j\)th fold as a validation set, and the remaining \(k - 1\) folds as training set
2.2 Estimate some measure of generalization error over the validation set
Average over the \(k\) estimates of the generalization error
Properties
Computational cost depends on \(k\), as we need to fit each model in the candidate set \(k\) times!
For \(k = n\), we get leave-one-out cross validation, which has good bias properties but may have high variance (and high computational cost for general model classes).
As \(k\) decreases we trade-off bias for a reduction in variance (and computational cost).1
Best \(m\) for mpg ~ poly(horsepower, m)
R code
n_reps <- 5
n_folds <- 5
cvs <- replicate(n_reps, cv(models(mods), k = n_folds, data = Auto), simplify = FALSE)
MSEcv <- sapply(cvs, function(cvfit) sapply(cvfit, function(x) x[["CV crit"]]))
crits <- data.frame(degree = degrees,
criterion = rep(c(paste0("MSE[split ", 1:n_splits, "]"),
paste0("MSE[CV rep ", 1:n_reps, "]"), "AIC"),
each = length(degrees)),
approach = rep(c("Validation set", "10-fold CV", "IC"), c(n_splits * length(degrees), n_reps * length(degrees), length(degrees))),
value = c(c(MSEv), c(MSEcv), AICs), check.names = FALSE)
crits <- crits |> group_by(criterion) |> mutate(value = value / min(value))
cols0 <- hcl.colors(11, palette = "Dynamic")
ggplot(crits,
aes(degree, value, col = criterion)) +
geom_line() + geom_point() +
theme_minimal() +
labs(y = "criterion / min(criterion)") +
lims(y = range(crits$value)) +
scale_x_continuous(breaks = 1:10) +
scale_color_manual(values = cols0) +
facet_wrap(~ approach, scales = "free_y")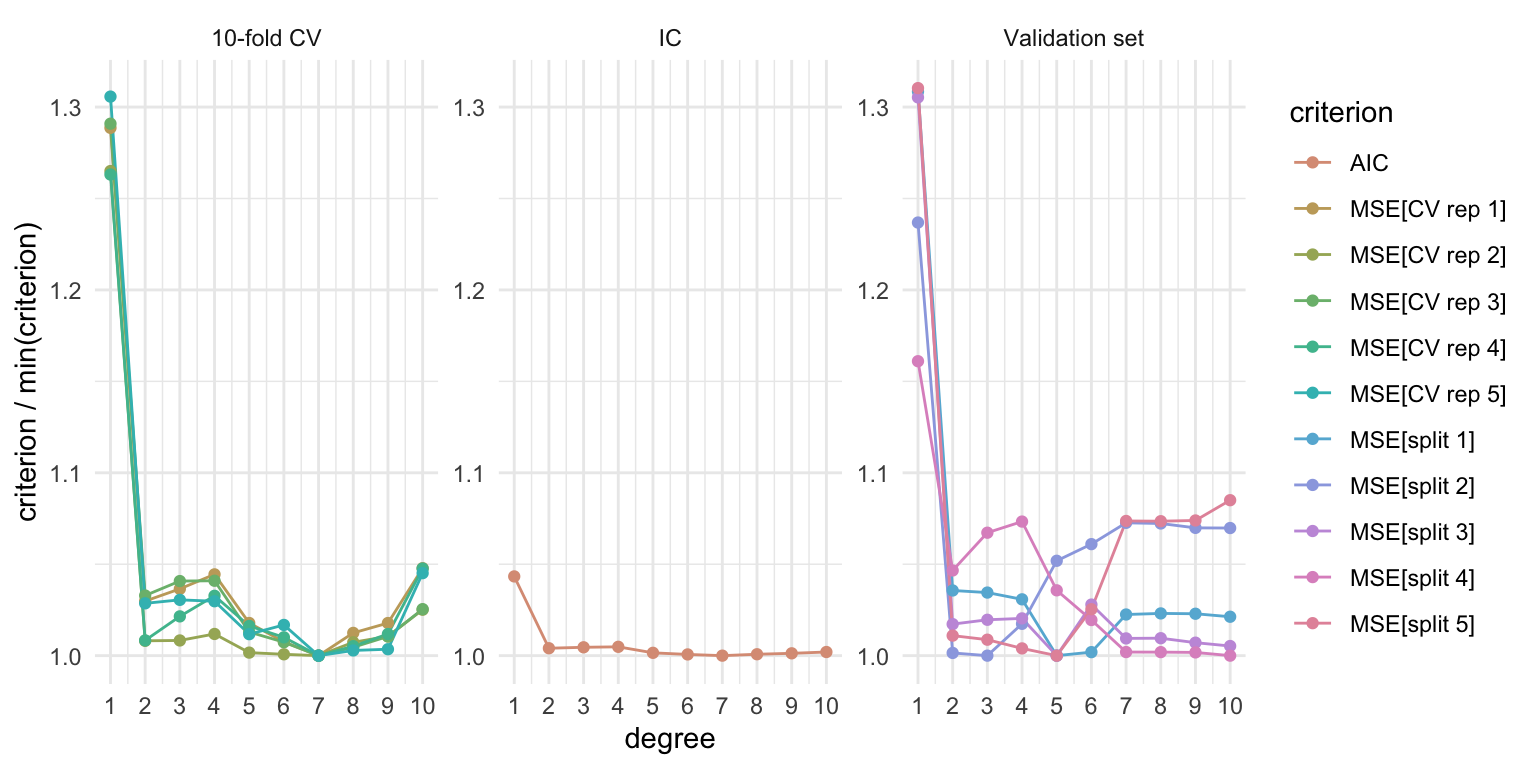
Leave-one-out cross validation: linear regression
For \(k = n\) (leave-one-out cross-validation), the estimator of \(\Delta\) is \[ \hat\Delta_\text{CV} = \frac{1}{n} \sum_{i=1}^n (y_i - x_i^\top \hat\beta_{-i})^2 \tag{10}\] where \(\hat\beta_{-j}\) is the estimate computed without the \(i\)th observation.
(10) suggests that we need \(n\) fits to compute \(\hat\Delta_\text{CV}\), which is true for general models. But, for linear models, it can be shown that \[ \hat\Delta_\text{CV} = \frac{1}{n} \sum_{i=1}^n \frac{(y_i - x_i^\top \hat\beta)^2}{(1 - h_{ii})^2} \] where \(h_{11},\ldots, h_{nn}\) are diagonal elements of \(H\).
Generalized cross validation
Another estimator of \(\Delta\) in mean regression settings uses generalized cross-validation and has the form \[ \hat\Delta_\text{GCV} = \frac{1}{n} \sum_{i = 1}^n \frac{(y_i - \hat{\psi}(x_i))^2}{\{1 - \mathop{\mathrm{tr}}(\hat{H})/n\}^2} \] where \(\hat{\psi}(x_i)\) is an estimator of \(\mathop{\mathrm{E}}(Y_i \mid x_i)\), with \(\hat{H}\) a projection matrix from \(Y_i\) to \(\hat{\psi}(x_i)\).1
For linear regression models we have \[ \mathop{\mathrm{E}}(\hat \Delta_\text{GCV}) = \frac{1}{n(1 - p / n)^2} \mu^\top (I_n - H)\mu + \frac{1}{1 - p / n} \sigma^2 \, . \] For fixed \(p\) and large \(n\), \(\mathop{\mathrm{E}}(\hat \Delta_\text{GCV}) \approx \Delta\).2
Generalized cross validation
Proof. It holds that \(Y - X\hat\beta = (I_n - H) Y = (I_n - H) \mu + (I_n - H) \epsilon\). So, \[ (Y - X\hat\beta)^\top (Y - X\hat\beta) = {\color[rgb]{0.5,0.5,1}{\mu^\top (I_n - H) \mu + \epsilon^\top (I_n - H) \epsilon + Z}} \] where the terms collected in \(Z\) have expectation zero. Using the fact that \(\mathop{\mathrm{tr}}{H} = p\), \[ \begin{aligned} \mathop{\mathrm{E}}(\hat \Delta_\text{GCV}) & = {\color[rgb]{0.5,0.5,1}{\frac{1}{n(1 - p / n)^2}\mu^\top (I_n - H) \mu + \frac{(n - p)}{n(1 - p / n)^2} \sigma^2}} \\ & = {\color[rgb]{0.5,0.5,1}{\frac{1}{n(1 - p / n)^2} \mu^\top (I_n - H) \mu + \frac{1}{1 - p/n}\sigma^2}} \end{aligned} \tag{11}\]
For large \(n\) or small \(z = 1 / n\), a Taylor expansion of \((1 - p z)^{-1}\) about \(z = 0\) gives \((1 - p z)^{-1} = {\color[rgb]{0.5,0.5,1}{1 + p z + O(z^2)}}\). Also, \(z (1 - z p)^{-2} = {\color[rgb]{0.5,0.5,1}{z + O(z^2)}}\). Replacing \((1 - p/n)^{-1}\) and \(n^{-1}(1 - p / n)^{-2}\) in the last expression in (11) with their first order approximations gives \[ \Delta = \mu (I_n - H) \mu / n + (1 + p / n) \sigma^2 \]
Some notable works on information criteria
Deviance information criterion
Spiegelhalter et al. (2002) propose minimizing the deviance information criterion \(DIC_m = -2\log f(y \mid \bar{\theta}_m, m) + 2p_{D, m}\), where \(\bar\theta_m = \mathop{\mathrm{E}}(\theta_m \mid y, m)\) and \[ p_{D, m} = -2 \int \left\{\log f(y \mid \bar{\theta}_m, m) - \log f(y \mid \theta_m, m)\right\} \pi(\theta_m \mid y, m) d \theta \] is the “effective number of parameters”. Despite Bayesian in nature, DIC is more similar to AIC than BIC. In fact, under regularity conditions DIC and TIC are asymptotically equivalent1.
Singular models
Drton & Plummer (2017)2 develop the singular BIC as a consistent criterion aim at \(\max \pi(m \mid y)\), when the candidates include models whose Fisher information matrices may not be invertible along other candidates (e.g. selection of the number of mixture components, rank in reduced-rank regression, number of factors in factor analysis, etc).
Some notable works on information criteria
Overviews
Lahiri (2001) has a collection of excellent reviews of model selection procedures based on information criteria with particular focus on regression settings. The contribution by Rao and Wu (pages 1-64) is of particular note.
Zhang et al. (2023) is a recent, accessible review of advances in information criteria, focusing on their derivation, properties and connections, and arguing against common misconceptions.
Some notable works on information criteria
Consistent information criteria for high-dimensional regression
Kim et al. (2012)1 study a family of information criteria in linear regression models with high-dimensional covariates, and develop sufficient conditions about the error variance estimator and the information criteria, for model selection by minimizing the latter to be consistent.
Focuced information criterion
Claeskens & Hjort (2003) define the focused information criterion, which can identify the best model for the estimation of a “focus” parameter. Different focus parameters can lead to the selection of different best models.
Some notable works on information criteria
Robustification of AIC procedures
Ronchetti (1997) point out the sensitivity of AIC/TIC-like model selection procedures to outliers and other departures from distributional assumptions, and derive a robust version of AIC information criterion.
Konishi & Kitagawa (1996) use influence functions to derive a generalized information criterion that applies to general \(M\)-estimation problems, including robust regression, maximum (penalized) likelihood estimation and some Bayes procedures.
BIC for large model spaces
Chen & Chen (2008) develop an extended family of Bayesian information criteria, which take into account both the number of unknown parameters and the complexity of the model space. These criteria result in consistent model selection under mild conditions even when \(p\) grows with \(n\), and have been found to control the false discovery rate with a small loss in the positive selection rate.
Non-parametric and semi-parametric estimation
Simonoff & Tsai (1999) develop an AIC\(_c\)-like criterion for use in semiparametric and additive regression models.
Some notable works on variable selection
Bayesian variable selection and model averaging
Li & Clyde (2018) introduce a unified framework for mixtures of \(g\)-priors for Bayesian variable selection and model averaging using GLMs that generalizes a number of previous works, and argue in terms of model selection properties. They derive analytical approximations to the marginal likelihoods, which also lead to information criteria.
Selection and estimation through shrinkage
Tibshirani (1996) introduces the lasso (least absolute shrinkage and selection operation), which penalizes the log-likelihood of a regression model by the \(\ell\)_1 norm of the regression coefficients. Such a construct allows for simultaneous variable selection and estimation through a convex problem if the negative log-likelihood is convex, and hence is attractive both theoretically and computationally. Book level treatments of the lasso and its numerous extensions, alternatives, and associated topics can be found at Hastie et al. (2015) and Hastie et al. (2017).
| Materials | Link |
|---|---|
| Preliminary material | ikosmidis.com/files/APTS-SM-Preliminary |
| Notes | ikosmidis.com/files/APTS-SM-Notes |
| Slides: Model selection | ikosmidis.com/files/APTS-SM-Slides-model-selection.html |
| Slides: Beyond GLMs | ikosmidis.com/files/APTS-SM-Slides-beyond-glms.html |
| Slides: Nonlinear models | ikosmidis.com/files/APTS-SM-Slides-nonlinear-models.html |
| Slides: Latent variables | ikosmidis.com/files/APTS-SM-Slides-latent.html |
| Lab 1 | ikosmidis.com/files/APTS-SM-Notes/lab1.html |
| Lab 2 | ikosmidis.com/files/APTS-SM-Notes/lab2.html |
References

Ioannis Kosmidis - Statistical Modelling: Model Selection



