6  Lab 2 (with solution)

6.1 Exercise

The data in hip.txt are from Crowder & Hand (1990), and we can put them in an R data.frame by

hip_url <- url("https://ikosmidis.com/files/APTS-SM-Notes/resources/hip.txt")
hip <- read.table(hip_url,
                  col.names = c("y", "age", "sex", "subj", "time"),
                  colClasses = c(rep("numeric", 4), "factor"))
str(hip)
'data.frame':   88 obs. of  5 variables:
 $ y   : num  47.1 31.1 32.8 44.1 31.5 ...
 $ age : num  66 66 66 70 70 70 44 44 44 70 ...
 $ sex : num  0 0 0 0 0 0 0 0 0 0 ...
 $ subj: num  1 1 1 2 2 2 3 3 3 4 ...
 $ time: Factor w/ 3 levels "1","2","3": 1 2 3 1 2 3 1 2 3 1 ...

The variable y contains measurements of haematocrit on 30 patients (subj) on up to three occasions (time), one before a hip-replacement operation (coded as 1), and two afterwards (coded as 2 and 3). time is treated here as a categorical variable. The age and sex (0 for male, 1 for female) of the patients are also recorded.

The primary interest in this study is in possible differences in the evolution of haematocrit between males and females and whether there is an age effect.

  1. For each value of sex, plot the time profiles of the response variable for each subject.

    Do you think you think it is necessary to include a random intercept for the subject? What about a random slope for time?

  2. We will analyse these data using linear mixed models (LMMs) of the form \[ \begin{aligned} Y_{ij} \mid x_{ij}, z_{ij} & \stackrel{\text{ind}}{\sim}\mathop{\mathrm{N}}(\mu_{ij}, \sigma^2) \,,\\ \mu_{ij} & = x_{ij}^\top \beta + z_{ij}^\top b_i \,, \\ b_i & \stackrel{\text{ind}}{\sim}\mathop{\mathrm{N}}(0, \Sigma_b^*) \,, \end{aligned} \tag{6.1}\] where \(Y_{ij}\) is the random variable corresponding to the haematocrit measurement for subject \(i\) at time \(j\), and \(x_{ij}\) and \(z_{ij}\) are fixed-effects and mixed-effects covariates, respectively.

    Consider building a set of candidate LMMs for explaining haematocrit, using the fixed-effects of age, sex and time (and possibly interactions of sex to age and time) and random-effects of subj and time. If you want to have models with interaction effects in your candidate set, make sure that you respect the “marginality constraints”, that is the model should have main effects for all terms from which interactions are formed.

    What is your chosen model?

  3. For the model you chose, plot the predicted haematocrit for each patient against time.

    Use your chosen model to predict the full haematocrit profiles of any patients that do not have haematocrit measurements at all three time points.

Hints for plotting

For plotting, you may adapt the code used for producing Figure 2.2 for the rat growth data, or you may use the ggplot2 R package.

Hints for modelling

LMMs for clustered data can be fitted in R using the lmer() function from the lme4 package. For example,

library(lme4)
hip_lmm1 <- lmer(y ~ age + sex + time + (1 | subj), data = hip)

fits the model with \(x_{ij} = (1, \text{age}_i, \text{sex}_i, I(\text{time}_{ij} = 2), I(\text{time}_{ij} = 3))^\top\), and \(z_{ij} = 1\).

The default estimation method in lmer() is REML. If you want to obtain maximum likelihood estimates (for example, for use in model comparison), they can be obtained using the additional argument REML = FALSE.

You might find useful some of the following methods for the object that lmer() returns: summary, fitted, residuals, fixef (fixed effects estimates), ranef (random effects estimates), VarCorr (variance estimates) coef (coefficient estimates at cluster level, incorporating fixed and random effects), AIC, BIC and predict.

For more information, see ?lmer.

Quantities in the general LMM definiton in (2.5)

In terms of the general definition of LMMs in (2.5), in order to get a better understanding of what the formula interface of lmer() does, for hip_lmm1, \(Y\) is

mf1 <- model.frame(hip_lmm1)
model.response(mf1)
    1     2     3     4     5     6     7     8     9    10    11    12    13 
47.10 31.05 32.80 44.10 31.50 37.00 39.70 33.70 24.50 43.30 18.35 36.60 37.40 
   14    15    16    17    18    19    20    21    22    23    24    25    26 
32.25 29.05 45.70 35.50 39.80 44.90 34.10 32.05 42.90 32.05 46.05 28.80 37.80 
   27    28    29    30    31    32    33    34    35    36    37    38    39 
42.10 34.40 36.05 38.25 29.40 30.50 43.00 33.70 36.65 37.80 26.60 30.60 37.25 
   40    41    42    43    44    45    46    47    48    49    50    51    52 
26.50 38.45 27.95 33.95 27.00 32.50 31.95 38.35 32.30 37.90 38.80 32.55 26.85 
   53    54    55    56    57    58    59    60    61    62    63    64    65 
44.65 32.25 34.20 38.00 27.10 37.85 34.00 23.20 25.95 44.80 37.20 29.70 45.95 
   66    67    68    69    70    71    72    73    74    75    76    77    78 
29.10 26.70 41.85 31.95 37.60 38.00 31.65 35.70 42.20 34.00 33.25 39.70 33.45 
   79    80    81    82    83    84    85    86    87    88 
32.65 37.50 28.20 30.30 34.55 30.95 28.75 35.50 24.70 29.75

\(X\) is

model.matrix(hip_lmm1, type = "fixed")
   (Intercept) age sex time2 time3
1            1  66   0     0     0
2            1  66   0     1     0
3            1  66   0     0     1
4            1  70   0     0     0
5            1  70   0     1     0
6            1  70   0     0     1
7            1  44   0     0     0
8            1  44   0     1     0
9            1  44   0     0     1
10           1  70   0     0     0
11           1  70   0     1     0
12           1  70   0     0     1
13           1  74   0     0     0
14           1  74   0     1     0
15           1  74   0     0     1
16           1  65   0     0     0
17           1  65   0     1     0
18           1  65   0     0     1
19           1  54   0     0     0
20           1  54   0     1     0
21           1  54   0     0     1
22           1  63   0     0     0
23           1  63   0     1     0
24           1  71   0     0     0
25           1  71   0     1     0
26           1  71   0     0     1
27           1  68   0     0     0
28           1  68   0     1     0
29           1  68   0     0     1
30           1  69   0     0     0
31           1  69   0     1     0
32           1  69   0     0     1
33           1  64   0     0     0
34           1  64   0     1     0
35           1  64   0     0     1
36           1  70   0     0     0
37           1  70   0     1     0
38           1  70   0     0     1
39           1  60   1     0     0
40           1  60   1     1     0
41           1  60   1     0     1
42           1  52   1     1     0
43           1  52   1     0     1
44           1  52   1     0     0
45           1  52   1     1     0
46           1  52   1     0     1
47           1  75   1     0     0
48           1  75   1     1     0
49           1  75   1     0     1
50           1  72   1     0     0
51           1  72   1     1     0
52           1  72   1     0     1
53           1  54   1     0     0
54           1  54   1     1     0
55           1  54   1     0     1
56           1  71   1     0     0
57           1  71   1     1     0
58           1  71   1     0     1
59           1  58   1     0     0
60           1  58   1     1     0
61           1  58   1     0     1
62           1  77   1     0     0
63           1  77   1     1     0
64           1  77   1     0     1
65           1  66   1     0     0
66           1  66   1     1     0
67           1  66   1     0     1
68           1  53   1     0     0
69           1  53   1     1     0
70           1  53   1     0     1
71           1  74   1     0     0
72           1  74   1     1     0
73           1  74   1     0     1
74           1  78   1     0     0
75           1  78   1     1     0
76           1  78   1     0     1
77           1  74   1     0     0
78           1  74   1     1     0
79           1  74   1     0     1
80           1  79   1     0     0
81           1  79   1     1     0
82           1  79   1     0     1
83           1  71   1     0     0
84           1  71   1     1     0
85           1  71   1     0     1
86           1  68   1     0     0
87           1  68   1     1     0
88           1  68   1     0     1
attr(,"assign")
[1] 0 1 2 3 3
attr(,"contrasts")
attr(,"contrasts")$time
[1] "contr.treatment"

attr(,"msgScaleX")
character(0)

and \(Z\) is

model.matrix(hip_lmm1, type = "random")
88 x 30 sparse Matrix of class "dgCMatrix"
  [[ suppressing 30 column names '1', '2', '3' ... ]]
                                                              
1  1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2  1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3  1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4  . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5  . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6  . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7  . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . .
8  . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . .
9  . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . .
10 . . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . .
11 . . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . .
12 . . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . .
13 . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . . .
14 . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . . .
15 . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . . .
16 . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . .
17 . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . .
18 . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . .
19 . . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . .
20 . . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . .
21 . . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . .
22 . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . . .
23 . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . . .
24 . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . .
25 . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . .
26 . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . .
27 . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . .
28 . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . .
29 . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . .
30 . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . .
31 . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . .
32 . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . .
33 . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . .
34 . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . .
35 . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . .
36 . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . .
37 . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . .
38 . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . .
39 . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . .
40 . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . .
41 . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . .
42 . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . .
43 . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . .
44 . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . .
45 . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . .
46 . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . .
47 . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . .
48 . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . .
49 . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . .
50 . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . .
51 . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . .
52 . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . .
53 . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . .
54 . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . .
55 . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . .
56 . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . .
57 . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . .
58 . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . .
59 . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . .
60 . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . .
61 . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . .
62 . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . .
63 . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . .
64 . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . .
65 . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . .
66 . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . .
67 . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . .
68 . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . .
69 . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . .
70 . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . .
71 . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . .
72 . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . .
73 . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . .
74 . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . .
75 . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . .
76 . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . .
77 . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . .
78 . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . .
79 . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . .
80 . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . .
81 . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . .
82 . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . .
83 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 .
84 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 .
85 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 .
86 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
87 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
88 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

6.2 Solution

library("ggplot2")
hip_pl <- ggplot(hip) +
    geom_line(aes(time, y, group = subj), col = "grey") +
    geom_point(aes(time, y), fill = "#ff7518", pch = 21, col = "grey") +
    facet_grid(~ sex, labeller = label_both) +
    labs(y = "haematocrit", x = "Time") +
    theme_bw() +
    labs(title = "Haematocrit")
hip_pl

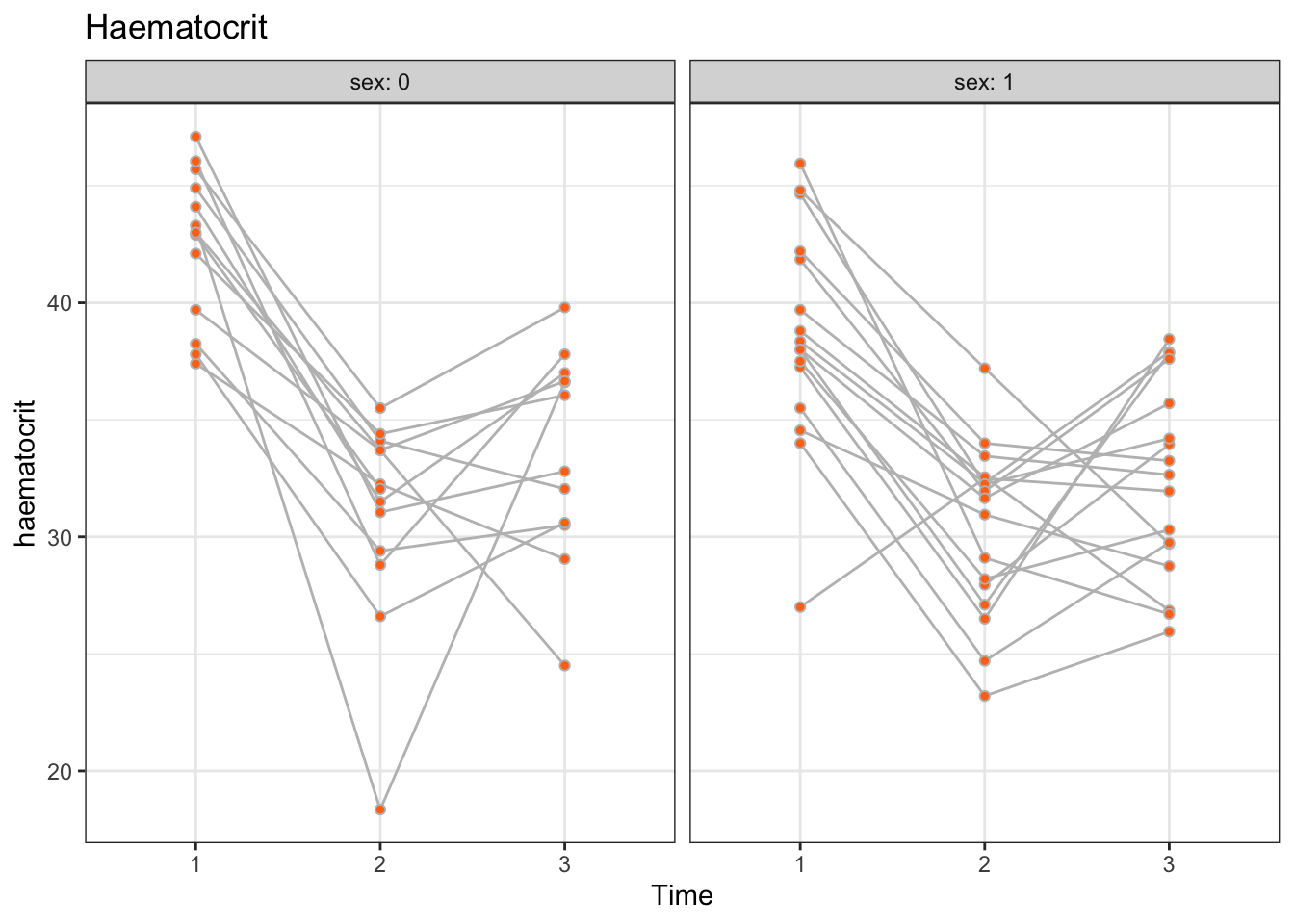
There appears to be heterogeneity between patients for both males and females. We observe no profound differences in profiles between males and females, perhaps apart from males having slightly elevated haematocrit levels. Also, with a few exceptions, the profiles appear to be roughly parallel across patients, or, equivalently, there appears to be no substantial heterogeneity in time.

Let’s fit all possible nested models of the model that includes an interaction of sex with age and time for the fixed effects, and random effects for patient, time or both patient and time, and compute the AIC and BIC for each model. In doing so, we need to respect marginality constraints. In other words, the list of candidate models should include all possible models with main effects (2^3 = 8 in that case), and from the models with interactions we should include only those that include their respective main effects. We can easily list the resulting set of candidate models for the fixed-effects in that case:

Main effects only Interactions and respective main effects
y ~ 1
y ~ age
y ~ sex
y ~ time
y ~ age + sex y ~ age + sex + age:sex
y ~ age + time
y ~ sex + time y ~ sex + time + sex:time
y ~ age + sex + time y ~ age + sex + time + age:time
y ~ age + sex + time + sex:time
y ~ age + sex + time + sex:time + age:time

We can now include the above model formulas in R in a list, after adding a random intercept for patient, and use a for loop to fit all models using lmer() with REML = FALSE, and compute AIC, BIC and AICc for each model.

Instead, we can simply fit the model with all interactions with REML = FALSE, and use the dredge() function of the MuMIn R package to compute information criteria for all other models, as we did in Example 1.2 with linear models for the nodal involvement data. dredge() is convenient because marginality constraints are respected; see ?dredge.

The code chunk below does that for AIC, BIC, and AICc.

library("MuMIn")
hip_full_subj <- lmer(y ~ sex * (age + time) + (1 | subj), data = hip,
                      REML = FALSE,
                      na.action = "na.fail")
ms <- dredge(hip_full_subj, rank = "AIC", extra = c("AIC", "AICc", "BIC"))
ms
Global model call: lmer(formula = y ~ sex * (age + time) + (1 | subj), data = hip, 
    REML = FALSE, na.action = "na.fail")
---
Model selection table 
   (Int)       age    sex tim age:sex sex:tim   AIC  AICc   BIC df   logLik
7  41.38           -1.860   +                 507.1 508.2 522.0  6 -247.574
23 42.48           -3.861   +               + 507.9 509.7 527.7  8 -245.952
5  40.35                    +                 508.4 509.2 520.8  5 -249.212
8  39.08 0.0351800 -1.918   +                 508.8 510.2 526.1  7 -247.380
24 40.04 0.0375300 -3.941   +               + 509.5 511.8 531.8  9 -245.731
6  38.68 0.0250900          +                 510.2 511.3 525.1  6 -249.122
16 41.25 0.0018280 -5.281   + 0.05108         510.6 512.4 530.4  8 -247.286
32 42.34 0.0022280 -7.506   + 0.05404       + 511.3 514.1 536.0 10 -245.626
3  35.71           -2.010                     567.7 568.2 577.7  4 -279.873
1  34.57                                      568.3 568.6 575.7  3 -281.142
4  32.60 0.0477400 -2.092                     569.3 570.0 581.7  5 -279.647
2  32.16 0.0363400                            570.0 570.5 579.9  4 -281.014
12 35.68 0.0004708 -6.880     0.07267         571.1 572.1 585.9  6 -279.527
     AIC delta weight
7  507.1  0.00  0.286
23 507.9  0.76  0.196
5  508.4  1.28  0.151
8  508.8  1.61  0.128
24 509.5  2.31  0.090
6  510.2  3.10  0.061
16 510.6  3.43  0.052
32 511.3  4.10  0.037
3  567.7 60.60  0.000
1  568.3 61.14  0.000
4  569.3 62.15  0.000
2  570.0 62.88  0.000
12 571.1 63.91  0.000
Models ranked by AIC(x) 
Random terms (all models): 
  1 | subj
Fixed term is "(Intercept)"
boundary (singular) fit: see help('isSingular')
boundary (singular) fit: see help('isSingular')
boundary (singular) fit: see help('isSingular')
boundary (singular) fit: see help('isSingular')
boundary (singular) fit: see help('isSingular')

We see that AIC and AICc agree that the best model is the model with main effects for sex and time and a patient-specific random intercept. That model is only second-best in terms of BIC (BIC of 522.01) after the model with with a main effect of only time (BIC of 520.81).

So, from the models with patient-specific intercepts, there is evidence for the model y ~ sex + time + (1 | subj).

Let’s try to do the same including a patient-specific random slope for time in the model:

hip_full_subj_time <- lmer(y ~ sex * (age + time) + (time | subj), data = hip,
                           REML = FALSE,
                           na.action = "na.fail")
Error: number of observations (=88) <= number of random effects (=90) for term (time | subj); the random-effects parameters and the residual variance (or scale parameter) are probably unidentifiable

We get an error message, because there are now too many different random effect terms in the model to be able to estimate them all from the data available.

Let’s fit the chosen model using REML

hip_mod <- lmer(y ~ sex + time + (1 | subj), data = hip)
summary(hip_mod)
Linear mixed model fit by REML ['lmerMod']
Formula: y ~ sex + time + (1 | subj)
   Data: hip

REML criterion at convergence: 489.5

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.1899 -0.5637  0.0305  0.6154  1.6744 

Random effects:
 Groups   Name        Variance Std.Dev.
 subj     (Intercept)  2.92    1.709   
 Residual             14.55    3.815   
Number of obs: 88, groups:  subj, 30

Fixed effects:
            Estimate Std. Error t value
(Intercept)  41.3847     0.9661  42.838
sex          -1.8600     1.0360  -1.795
time2        -9.7657     0.9947  -9.817
time3        -7.3572     1.0047  -7.323

Correlation of Fixed Effects:
      (Intr) sex    time2 
sex   -0.596              
time2 -0.518 -0.011       
time3 -0.504 -0.026  0.505

We can use the predict() method to get predictions for the haematocrit profiles of the patients in the sample, and compare them to the observed profiles.

hip_pred <- within(hip, y <- predict(hip_mod))
hip$type <- "observed"
hip_pred$type <- "predicted"
ggplot(rbind(hip, hip_pred)) +
    geom_point(aes(time, y, fill = type), pch = 21, col = "lightgray") +
    geom_line(aes(time, y, group = subj), col = "lightgray") +
    facet_grid(type ~ sex, labeller = label_both) +
    labs(y = "haematocrit", x = "Time") +
    theme_bw()

In order to identify the patients with missing haematocrit measurements, we check which patients do not have all 3 times in the data.

id_na <- which(tapply(hip, hip$subj, function(x) !all(1:3 %in% x$time)))
hip_na <- subset(hip, subj %in% id_na)
hip_na
       y age sex subj time     type
22 42.90  63   0    8    1 observed
23 32.05  63   0    8    2 observed
42 27.95  52   1   15    2 observed
43 33.95  52   1   15    3 observed

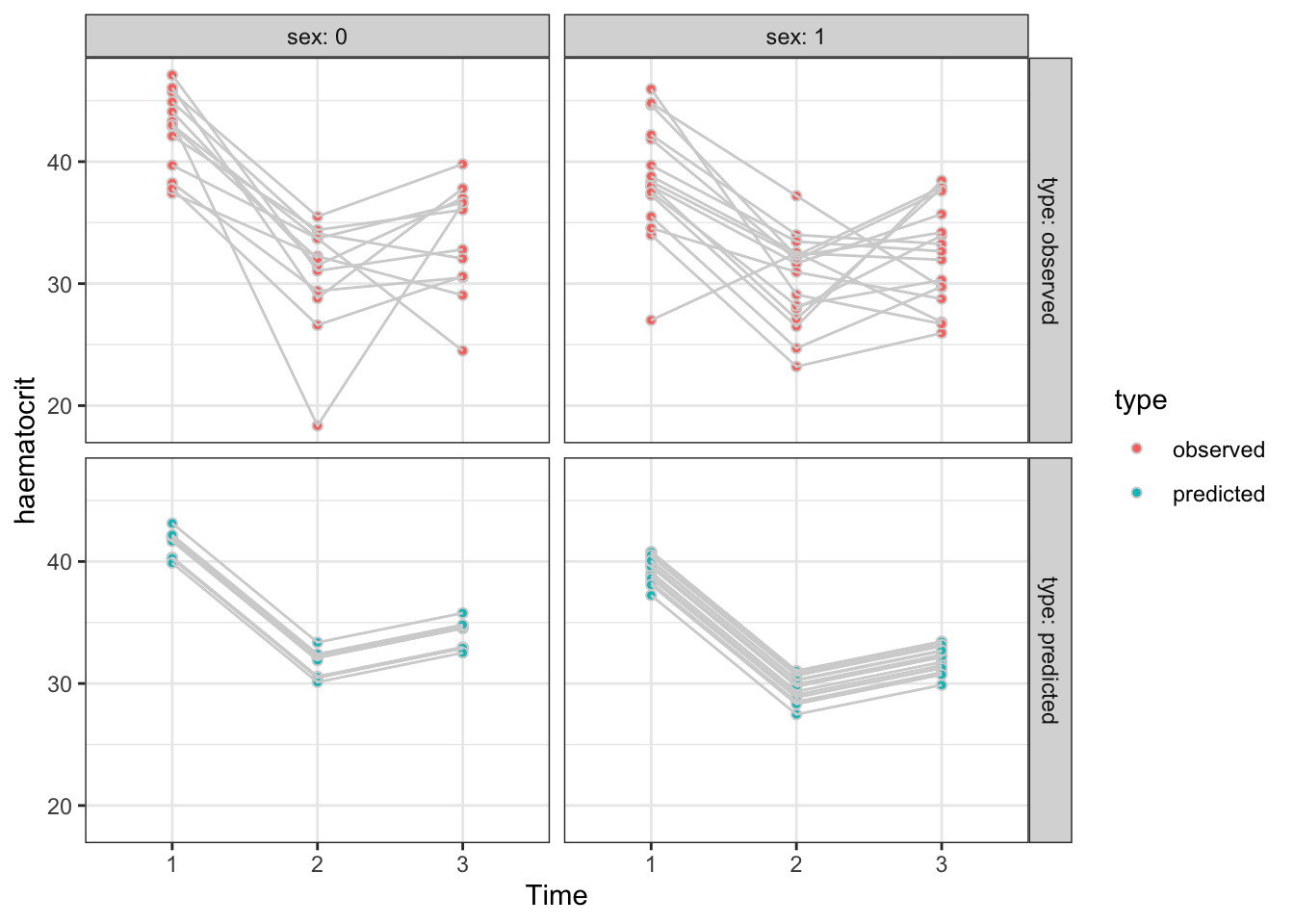
Since the chosen model only involves sex, time and subject, we want to predict the haematocrit levels for every row of the data frame

## Get unique sex/subject combinations for the two patients with missing
## data
new_data <- unique(hip_na[c("sex", "subj")])
## Add time
new_data <- rbind(data.frame(time = factor(1:3), new_data[1, ]),
                  data.frame(time = factor(1:3), new_data[2, ]))
new_data
  time sex subj
1    1   0    8
2    2   0    8
3    3   0    8
4    1   1   15
5    2   1   15
6    3   1   15

The predictions are

new_data$y <- predict(hip_mod, newdata = new_data)
new_data
  time sex subj        y
1    1   0    8 41.66335
2    2   0    8 31.89765
3    3   0    8 34.30619
4    1   1   15 39.52090
5    2   1   15 29.75520
6    3   1   15 32.16374

We can plot the observed and the predicted levels for the two patients

new_data$type <- "predicted"
hip_na$type <- "observed"
ggplot(rbind(new_data, hip_na[names(new_data)])) +
    geom_point(aes(time, y, fill = type), pch = 21, col = "lightgray") +
    geom_line(aes(time, y, group = interaction(subj, type)), col = "lightgray") +
    facet_grid( ~ sex, labeller = label_both) +
    labs(y = "haematocrit", x = "Time") +
    theme_bw()