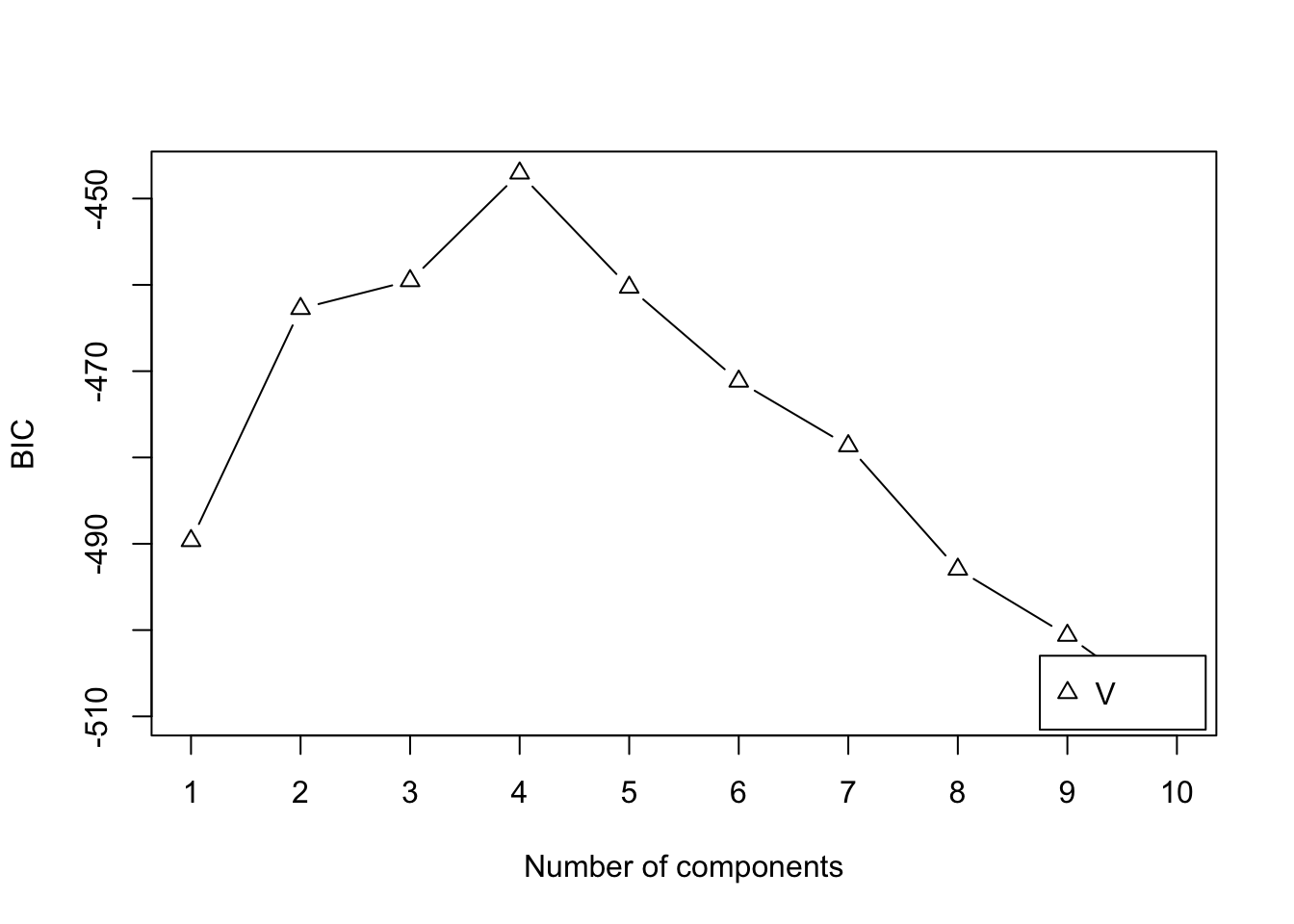
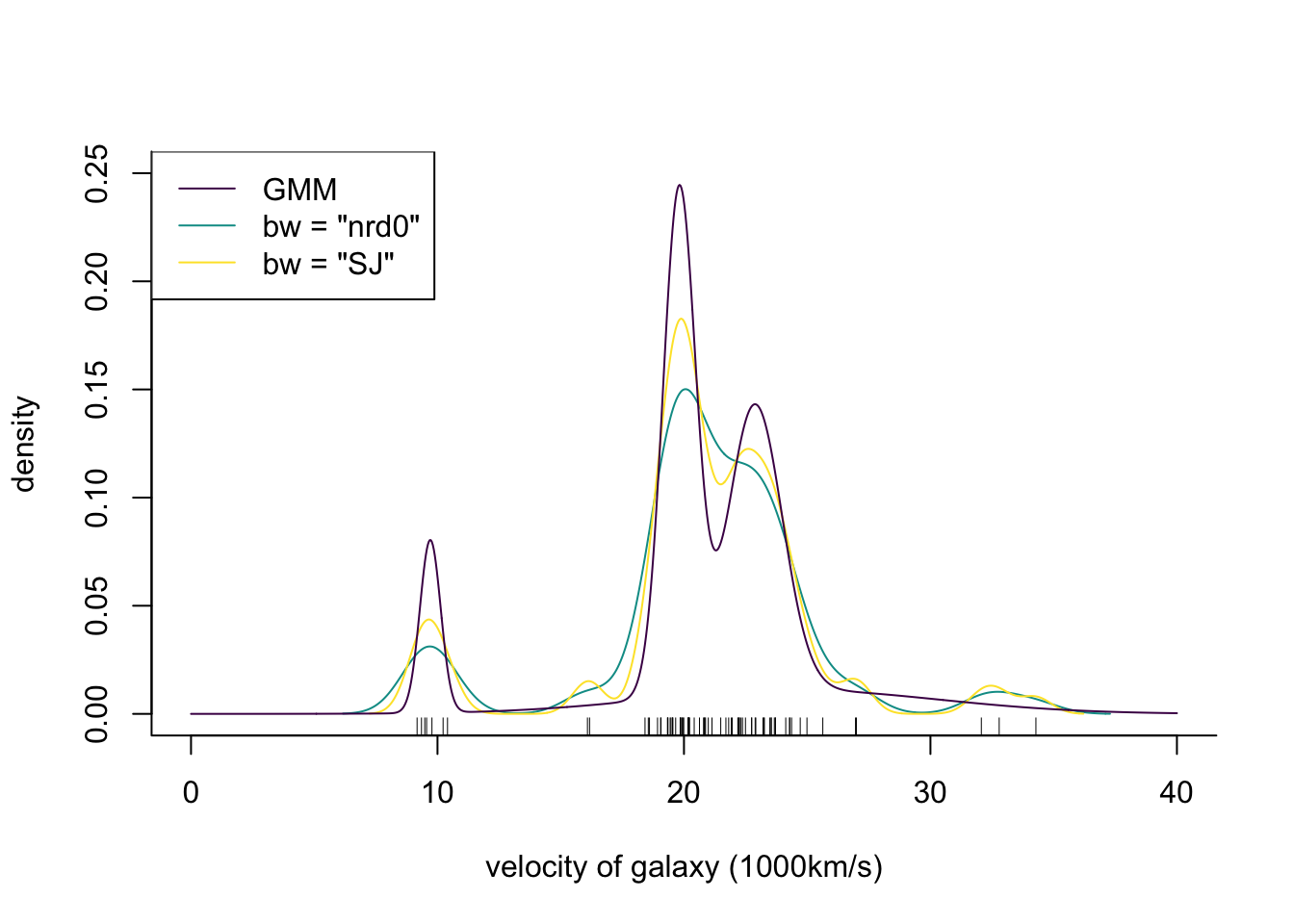
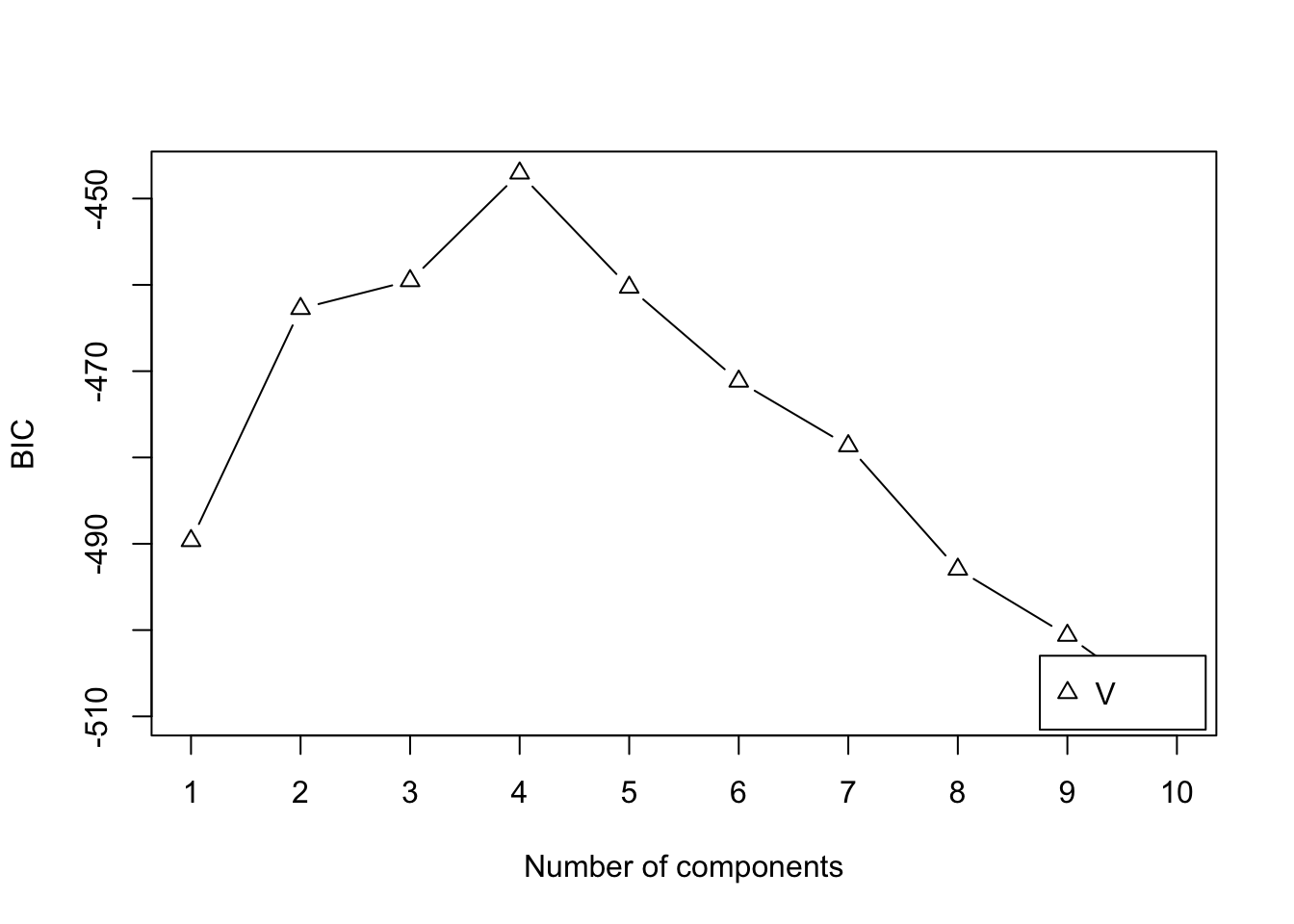
Suppose that the complete-data log likelihood is the logarithm of the density or probability mass function of an exponential family distribution, that is \[
\log f(y,u \,;\,\theta) = s(y,u)^\top\theta - \kappa(\theta) + c(y,u) \, .
\tag{4.6}\]
Akaike, H. (1973). Information theory and an extension of the maximum likelihood principle. In B. N. Petrov & F. Czáki (Eds.),
Second international symposium on information theory (pp. 267–281). Akad
emiai Kiad
ó.
https://doi.org/10.1007/978-1-4612-0919-5_38
Albert, J. H. (2007).
Bayesian computation with r. Springer-Verlag.
https://doi.org/10.1007/978-0-387-92298-0
Albert, J. H., & Chib, S. (1993). Bayesian analysis of binary and polychotomous response data.
Journal of the American Statistical Association,
88, 669–679.
https://doi.org/10.2307/2290350
Best, N., & Thomas, A. (2000). Bayesian graphical models and software for
GLMs. In D. K. Dey, S. K. Ghosh, & B. K. Mallick (Eds.),
Generalized linear models: A Bayesian perspective (pp. 387–406). Marcel Dekker.
https://doi.org/10.1201/9781482293456
Breslow, N. E., & Clayton, D. G. (1993). Appproximate inference in generalised linear mixed models.
Journal of the American Statistical Association,
88, 9–25.
https://doi.org/10.2307/2290687
Burnham, K. P., & Anderson, D. R. (2002).
Model selection and multi-model inference: A practical information theoretic approach (Second). Springer.
https://doi.org/10.1007/978-1-4757-2917-7
Candès, E., & Tao, T. (2007). The
Dantzig selector: Statistical estimation when
\(p\) is much larger than
\(n\) (with discussion).
Annals of Statistics,
35, 2313–2404.
https://doi.org/10.1214/009053606000001523
Claeskens, G., & Hjort, N. L. (2008).
Model selection and model averaging. Cambridge University Press.
https://doi.org/10.1017/CBO9780511790485
Cowell, R. G., Dawid, A. P., Lauritzen, S. L., & Spiegelhelter, D. J. (1999).
Probabilistic networks and expert systems. Springer-Verlag.
https://doi.org/10.1007/b97670
Crowder, M. J., & Hand, D. J. (1990).
Analysis of repeated measures. Chapman; Hall/CRC.
https://doi.org/10.1201/9781315137421
Davison, A. C. (2003).
Statistical models. Cambridge University Press.
https://doi.org/10.1017/CBO9780511815850
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the
EM algorithm (with discussion).
Journal of the Royal Statistical Society Series B,
39, 1–38.
https://doi.org/10.1111/j.2517-6161.1977.tb01600.x
Diggle, P. J., Heagerty, P., Liang, K.-Y., & Zeger, S. (2002).
Analysis of longitudinal data (2nd ed.). Oxford University Press.
https://global.oup.com/academic/product/analysis-of-longitudinal-data-9780199676750
Draper, D. (1995). Assessment and propagation of model uncertainty (with discussion).
Journal of the Royal Statistical Society Series B,
57, 45–97.
https://doi.org/10.1111/j.2517-6161.1995.tb02015.x
Efron, B. (1975). Defining the curvature of a statistical problem (with applications to second order efficiency).
The Annals of Statistics,
3(6), 1189–1242.
https://doi.org/10.1214/aos/1176343282
Fahrmeir, L., Kneib, T., Lang, S., & Marx, B. (Eds.). (2013).
Regression: Models, methods and applications. Springer.
https://doi.org/10.1007/978-3-642-34333-9
Fan, J., & Li, R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association, 96, 1348–1360.
Fan, J., & Lv, J. (2008). Sure independence screening for ultrahigh dimensional feature space (with
Discussion).
Journal of the Royal Statistical Society Series B,
70, 849–911.
https://doi.org/10.1198/016214501753382273
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2004).
Bayesian data analysis (3rd ed.). Chapman; Hall/CRC.
https://doi.org/10.1201/b16018
Gelman, A., Hill, J., & Vehtari, A. (2020).
Regression and other stories. Cambridge University Press.
https://doi.org/10.1017/9781139161879
Gilks, W. R., Richardson, S., & Spiegelhalter, D. J. (Eds.). (1996). Markov chain monte carlo in practice. Chapman & Hall.
Green, P. J., Hjørt, N. L., & Richardson, S. (Eds.). (2003).
Highly structured stochastic systems. Chapman & Hall/CRC.
10.1201/b14835
Hastie, T., Tibshirani, R., & Wainwright, M. (2015).
Statistical learning with sparsity: The Lasso and generalizations. Chapman; Hall/CRC.
https://doi.org/10.1201/b18401
Hoeting, J. A., Madigan, D., Raftery, A. E., & Volinsky, C. T. (1999). Bayesian model averaging: A tutorial (with discussion).
Statistical Science,
14, 382–417.
https://doi.org/10.1214/ss/1009212519
Jamshidian, M., & Jennrich, R. I. (1997). Acceleration of the
EM algorithm by using quasi-
Newton methods.
Journal of the Royal Statistical Society Series B,
59, 569–587.
https://doi.org/10.1111/1467-9868.00083
Kass, R. E., & Raftery, A. E. (1995). Bayes factors.
Journal of the American Statistical Association,
90, 773–795.
https://doi.org/10.1080/01621459.1995.10476572
Liang, K., & Zeger, S. L. (1986). Longitudinal data analysis using generalized linear models.
Biometrika,
73(1), 13–22.
https://doi.org/10.1093/biomet/73.1.13
Linhart, H., & Zucchini, W. (1986).
Model selection. Wiley.
https://doi.org/10.1007/978-3-642-04898-2_373
Little, R. J. A., & Rubin, D. B. (2002).
Statistical analysis with missing data (2nd ed.). Wiley.
https://doi.org/10.1002/9781119013563
Marin, J.-M., & Robert, C. P. (2007).
Bayesian core: A practical approach to computational bayesian statistics. Springer-Verlag.
https://doi.org/10.1007/978-0-387-38983-7
McCullagh, P. (2002). What is a statistical model?
The Annals of Statistics,
30(5), 1225–1310.
https://doi.org/10.1214/aos/1035844977
McCullagh, P., & Nelder, J. A. (1989).
Generalized linear models (2nd ed.). Chapman & Hall.
https://doi.org/10.1201/9780203753736
McCulloch, C. E., Searle, S. R., & Neuhaus, J. M. (2008).
Generalized, linear, and mixed models (2nd ed.). Wiley.
https://doi.org/10.1002/0471722073
McLachlan, G. J., & Krishnan, T. (2008).
The EM algorithm and extensions (2nd ed.). Wiley.
https://doi.org/10.1002/9780470191613
McQuarrie, A. D. R., & Tsai, C.-L. (1998).
Regression and time series model selection. World Scientific.
https://doi.org/10.1142/3573
Meng, X.-L., & van Dyk, D. (1997). The
EM algorithm — an old folk-song sung to a fast new tune (with discussion).
Journal of the Royal Statistical Society Series B,
59, 511–567.
https://doi.org/10.1111/1467-9868.00082
Nelder, J. A., Lee, Y., & Pawitan, Y. (2017).
Generalized linear models with random effects: A unified approach via \(h\)-likelihood (2nd ed.). Chapman; Hall/CRC.
https://doi.org/10.1201/9781315119953
Nelder, J. A., & Wedderburn, R. W. M. (1972). Generalized linear models.
Journal of the Royal Statistical Society: Series A (General),
135(3), 370–384.
https://doi.org/10.2307/2344614
O’Hagan, A., & Forster, J. J. (2004).
Kendall’s advanced theory of statistics. Volume 2B: Bayesian inference (Second). Hodder Arnold.
https://www.wiley.com/en-us/Kendall%27s+Advanced+Theory+of+Statistic+2B-p-9780470685693
Oakes, D. (1999). Direct calculation of the information matrix via the
EM algorithm.
Journal of the Royal Statistical Society Series B,
61, 479–482.
https://doi.org/10.1111/1467-9868.00188
Ogden, H. (2021). On the error in laplace approximations of high-dimensional integrals.
Stat,
10(1), e380.
https://doi.org/10.1002/sta4.380
Ogden, H. E. (2017). On asymptotic validity of naive inference with an approximate likelihood.
Biometrika,
104(1), 153–164.
https://doi.org/10.1093/biomet/asx002
Peters, J., Janzing, D., & Schlkopf, B. (2017).
Elements of causal inference: Foundations and learning algorithms. The MIT Press.
https://mitpress.mit.edu/books/elements-causal-inference
Pinheiro, J., & Bates, D. M. (2002).
Mixed effects models in S and S-PLUS. New York:Springer-Verlag.
https://doi.org/10.1007/b98882
Raftery, A. E., Madigan, D., & Hoeting, J. A. (1997). Bayesian model averaging for linear regression models.
Journal of the American Statistical Association,
92, 179–191.
https://doi.org/10.1080/01621459.1997.10473615
Richardson, S., & Green, P. J. (1997). On bayesian analysis of mixtures with an unknown number of components (with discussion).
Journal of the Royal Statistical Society Series B,
59, 731–792.
https://doi.org/10.1111/1467-9868.00095
Rissanen, J. (1987). Stochastic complexity (with discussion).
Journal of the Royal Statistical Society, Series B,
49, 223–239.
https://doi.org/10.1111/j.2517-6161.1987.tb01694.x
Schwartz, G. (1978). Estimating the dimension of a model.
Annals of Statistics,
6, 461–464.
https://doi.org/10.1214/aos/1176344136
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., & Linde, A. van der. (2002). Bayesian measures of model complexity and fit (with discussion).
Journal of the Royal Statistical Society, Series B,
64, 583–639.
https://doi.org/10.1111/1467-9868.00353
Tanner, M. A. (1996).
Tools for statistical inference: Methods for the exploration of posterior distributions and likelihood functions (Third). Springer.
https://doi.org/10.1007/978-1-4612-4024-2
Venables, W., & Ripley, B. D. (2002).
Modern applied statistics with S (4th ed.). Springer-Verlag.
https://doi.org/10.1007/978-0-387-21706-2
Wedderburn, R. W. M. (1974). Quasi-
Likelihood Functions,
Generalized Linear Models, and the
Gauss-Newton Method.
Biometrika,
61(3), 439.
https://doi.org/10.2307/2334725
Wood, S. N. (2017).
Generalized additive models: An introduction with r (2nd ed.). Chapman; Hall/CRC.
https://doi.org/10.1201/9781315370279