APTS Statistical Modelling
Model Selection

Ioannis Kosmidis

Professor of Statistics
Department of Statistics, University of Warwick

ioannis.kosmidis@warwick.ac.uk
ikosmidis.com   ikosmidis ikosmidis_

19 April 2024

Outline

• Model selection
• Criteria
• Linear models
• Bayesian model selection

George Box (1919 – 2013)

Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful.

in Box and Draper (1987). Empirical Model-Building and Response Surfaces, p. 74

Picture by DavidMCEddy at en.wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=14941622

Model selection

Task

Select a statistical model from a set of candidate models on the basis of data.

Principles for selection

Background knowledge

Choose models based on substantive knowledge (e.g. from previous studies), theoretical arguments, dimensional or other general considerations.

Robustness to departures from assumptions

Prefer models that provide valid inference even if some of their assumptions are invalid.

Quality of fit

Prefer models that perform well in terms of informal devices such as residuals and graphical assessments, or more formal or goodness-of-fit tests.

Parsimony

Look for the simplest models that are adequate descriptions of the data.

Set of candidate models

Defined based on background knowledge, mathematical or computational convenience.

Defined accounting for the trade-off between allowed flexibility and cardinality of the set of candidate models.

Linear regression

Data

Response values \(y_1, \ldots, y_n\), with \(y_i \in \Re\)

Covariate vectors \(x_1, \ldots, x_n\), with \(x_i = (x_{i1}, \ldots, x_{ip})^\top \in \Re^p\)

Model

\[ Y_i = \sum_{t = 1}^p \beta_t x_{it} + \epsilon_i \] where \(\mathop{\mathrm{E}}(\epsilon_i) = 0\) and \(\mathop{\mathrm{var}}(\epsilon_i) = \sigma^2 < \infty\)

Set of candidate models

For \(p = 30\), assuming that every model has an intercept parameter (\(x_{i1} = 1\)), the set of candidate models has about 537 million possible models, without even accounting for covariate transformations or interactions!

Logistic regression

Data

Response values \(y_1, \ldots, y_n\), with \(y_i \in \{0, 1\}\)

Covariate vectors \(x_1, \ldots, x_n\), with \(x_i = (x_{i1}, \ldots, x_{ip})^\top \in \Re^p\)

Model

\(Y_{1}, \ldots, Y_{n}\) conditionally independent with

\[ Y_i \mid x_i \sim \mathop{\mathrm{Bernoulli}}(\mu_i)\,, \quad \log \frac{\mu_i}{1 - \mu_i} = \eta_i = \sum_{t = 1}^p \beta_t x_{it} \]

Widely used for inference about covariate effects on probabilities, probability calibration, and prediction.

Set of candidate models

Same considerations as for linear regression.

Logistic regression likelihood

\[ \ell(\beta) = \sum_{i=1}^n y_i x_i^\top \beta - \sum_{i=1}^n \log\left\{1 + \exp( x_i^\top \beta)\right\} \]

We expect a good fit to be one that gives large maximized log-likelihood \(\hat \ell = \ell(\hat\beta)\) where \(\hat\beta\) is the maximum likelihood estimator

Nodal involvement: ?SMPracticals::nodal

The treatment strategy for a patient diagnosed with cancer of the prostate depend highly on whether the cancer has spread to the surrounding lymph nodes.

It is common to operate on the patient to get samples from the nodes which are then analysed under a microscope.

For a sample of 53 prostate cancer patients, a number of possible predictor variables were measured before surgery. The patients then had surgery to determine nodal involvement.

data("nodal", package = "SMPracticals")
str(nodal)

'data.frame':   53 obs. of  7 variables:
 $ m    : Named num  1 1 1 1 1 1 1 1 1 1 ...
  ..- attr(*, "names")= chr [1:53] "1" "2" "3" "4" ...
 $ r    : Named num  1 1 1 1 1 0 1 0 0 0 ...
  ..- attr(*, "names")= chr [1:53] "1" "2" "3" "4" ...
 $ aged : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
  ..- attr(*, "names")= chr [1:53] "1" "2" "3" "4" ...
 $ stage: Factor w/ 2 levels "0","1": 2 2 2 2 2 2 1 1 1 1 ...
  ..- attr(*, "names")= chr [1:53] "1" "2" "3" "4" ...
 $ grade: Factor w/ 2 levels "0","1": 2 2 2 2 2 2 1 1 1 1 ...
  ..- attr(*, "names")= chr [1:53] "1" "2" "3" "4" ...
 $ xray : Factor w/ 2 levels "0","1": 2 2 2 2 2 2 1 1 1 1 ...
  ..- attr(*, "names")= chr [1:53] "1" "2" "3" "4" ...
 $ acid : Factor w/ 2 levels "0","1": 2 2 2 2 2 2 2 2 2 2 ...
  ..- attr(*, "names")= chr [1:53] "1" "2" "3" "4" ...

Nodal involvement

Considering only the models with an intercept and without any interaction between the 5 binary covariates, results in \(2^5 = 32\) possible logistic regression models for this data.

library("SMPracticals")
library("MuMIn")
nodal_full <- glm(r ~ aged + stage + grade + xray + acid,
                  data = nodal, family = "binomial", na.action = "na.fail")
nodal_table <- dredge(nodal_full, rank = logLik)
plot(logLik ~ df, data = nodal_table,
     xlab = "Number of parameters",
     ylab = "Maximized log-likelihood",
     bg = "#ff7518", pch = 21)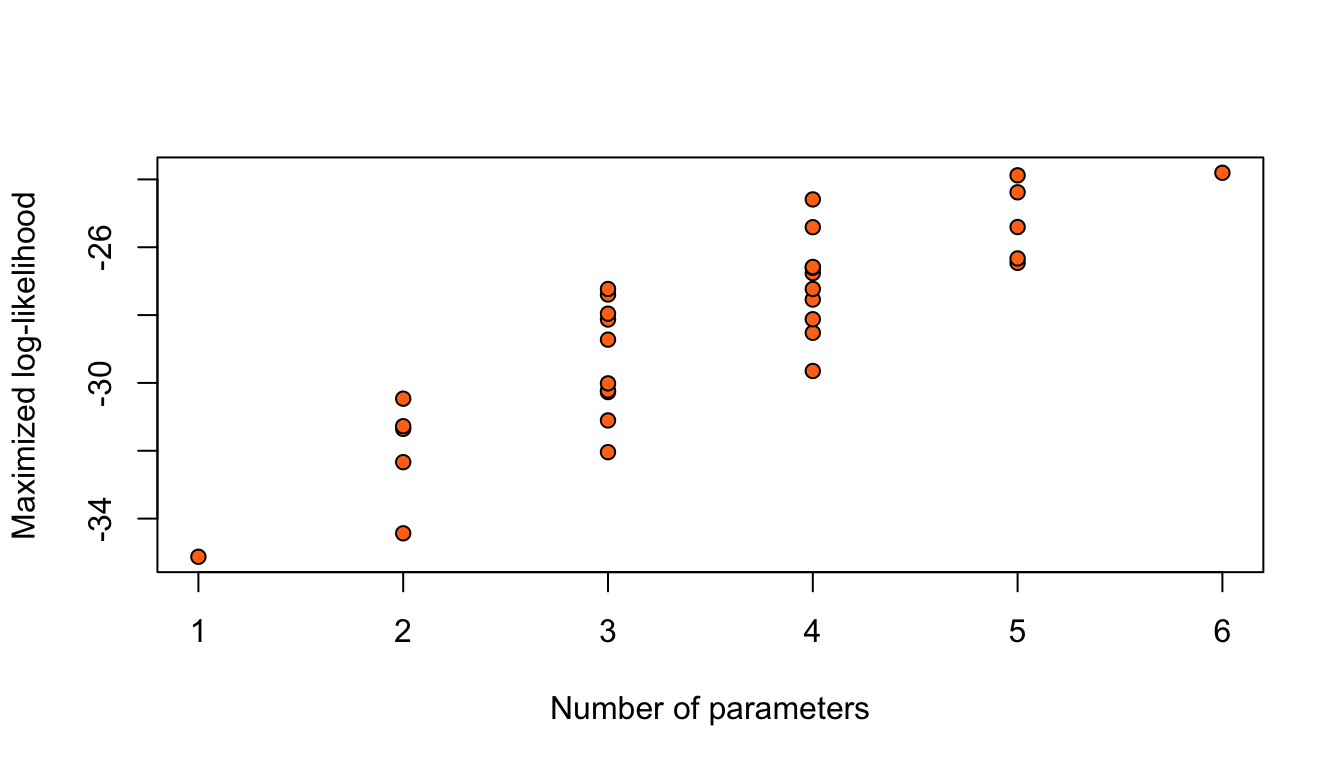

Figure 1: Maximized log-likelihoods for 32 possible logistic regression models for the nodal data.

Adding terms always increases the maximized log-likelihood.

Taking the model with highest \(\hat\ell\) would give the full model.

Linear regression

Let \(Y_i = \eta_i + \epsilon_i\). Removing terms always increases the residual sums of squares \(\|y - \hat{\eta} \|_2^2\).

• \(\eta_i = \beta_1 x_{i1} + \beta_2 x_{i2}\)
• \(\eta_i = \beta_2 x_{i2}\)
• \(\eta_i = \beta_1 x_{i1}\)

Criteria

Setting

True model

Independent \(Y_1, \ldots, Y_n\), where \(Y_i\) has a density or probability mass function \(g(y)\).

Candidate model

Independent \(Y_1, \ldots, Y_n\), where \(Y_i\) has a density or probability mass function \(f(y \,;\,\theta)\).

There may be no value of \(\theta\) such that \(f(\cdot \,;\,\theta) = g(\cdot)\).

Log-likelihood

Jensen’s inequality implies \[ \int \log g(y) g(y) dy \ge \int \log f(y \,;\,\theta) g(y) dy \tag{1}\] with equality if and only if \(f(y \,;\,\theta) = g(y)\).

If \(\theta_g\) is the value that maximizes the expectation in the right hand side of (1), then it is natural to choose the candidate model that maximizes the estimate of that expectation, i.e. \[ \bar\ell(\hat\theta) = n^{-1} \sum_{i = 1}^n \log f(y_i \,;\,\hat\theta) \]

However, by definition of \(\hat\theta\), \(\bar\ell(\hat\theta) \ge \bar\ell(\theta_g)\). So, \(\bar\ell(\hat\theta)\) is biased upwards.

Kullback-Leibler divergence

The log-likelihood \(\ell(\theta)\) of the candidate model is maximized at \(\hat\theta\), and \[ \bar \ell(\hat\theta) = n^{-1}\ell(\hat\theta) \to \int \log f(y \,;\,\theta_g) g(y)\, dy, \quad \text{as } n\to\infty \] where \(\theta_g\) minimizes the Kullback-Leibler divergence \[ KL(f_\theta,g) = \int \log\left\{ \frac{g(y)}{f(y \,;\,\theta)}\right\} g(y) \, dy \]

\(\theta_g\) gives the density \(f(y \,;\,\theta_g)\) closest to \(g(y)\), in this sense.

Inference under model misspecification

Asymptotic distribution of \(\hat\theta\)

Under mild regularity conditions, the maximum likelihood estimator \(\hat\theta\) satisfies \[ \sqrt{n} (\hat\theta - \theta_g) \stackrel{d}{\rightarrow} {\mathop{\mathrm{N}}}\left( 0, n I(\theta_g)^{-1}K(\theta_g)I(\theta_g)^{-1}\right) \tag{2}\] where \[ \begin{aligned} K(\theta) &= n \int \frac{\partial \log f(y \,;\,\theta)}{\partial\theta} \frac{\partial \log f(y \,;\,\theta)}{\partial\theta^\top }g(y)\, dy,\\ I(\theta) &= -n \int \frac{\partial^2 \log f(y \,;\,\theta)}{\partial\theta\partial\theta^\top } g(y)\, dy \end{aligned} \]

Inference under model misspecification

Likelihood ratio statistic

The likelihood ratio statistic converges in distribution as \[ W(\theta_g)=2\left\{\ell(\hat\theta)-\ell(\theta_g)\right\} \stackrel{d}{\rightarrow} \sum_{r=1}^p \lambda_r V_r \] where \(V_1, \ldots, V_p\) are independent with \(V_i \sim \chi^2_1\), and \(\lambda_r\) are eigenvalues of \(K(\theta_g)^{1/2}I(\theta_g)^{-1} K(\theta_g)^{1/2}\).

Thus, \(E\{W(\theta_g)\} \rightarrow \mathop{\mathrm{tr}}\{I(\theta_g)^{-1}K(\theta_g)\}\).

Inference under model misspecification

Estimating \(K(\theta_g)\) and \(I(\theta_g)\)

In practice \(g(y)\) is, of course, unknown, and \(K(\theta_g)\) and \(I(\theta_g)\) are estimated by \[ \hat K = \sum_{i=1}^n \frac{\partial \log f(y_i \,;\,\hat\theta)}{\partial\theta} \frac{\partial \log f(y_i \,;\,\hat\theta)}{\partial\theta^\top }, \quad \underbrace{\hat J = - \sum_{i=1}^n \frac{\partial^2 \log f(y_i \,;\,\hat\theta)} {\partial\theta\partial\theta^\top }}_{\text{observed information}} \]

Asymptotically valid inference

We can construct inferences about \(\theta_g\), using the fact that the approximate distribution of \(\hat\theta\) is \({\mathop{\mathrm{N}}}\left( \theta_g, I(\theta_g)^{-1}K(\theta_g)I(\theta_g)^{-1}\right)\), replacing the variance covariance matrix with \(\hat J^{-1}\hat K\hat J^{-1}\).

Maximum likelihood asymptotics under the true model

If \(g(\theta) = f(y \,;\,\theta_g)\), \(K(\theta) = I(\theta)\) and \(\lambda_1 = \ldots = \lambda_p = 1\), and we recover the usual results.

Out-of-sample prediction

Problems with using \(\bar\ell(\hat\theta)\) for model selection:

• Upward bias, as \(\bar\ell(\hat\theta) \ge \bar\ell(\theta_g)\) because \(\hat\theta\) is based on \(Y_1, \ldots, Y_n\)
• Improves quality of fit with no control over model complexity

If we had another independent sample \(Y_1^+,\ldots,Y_n^+\sim g\) and computed \[ \bar\ell^+(\hat\theta) = n^{-1}\sum_{i=1}^n \log f(Y^+_i \,;\,\hat\theta) \] then both problems disappear. In the limit, we choose the candidate model that maximizes \[ \Delta = {\mathop{\mathrm{E}}}_g\left[ {\mathop{\mathrm{E}}}^+_g\left\{ \bar\ell^+(\hat\theta) \right\} \right] \] where the inner expectation is over the distribution of \(Y_i^+\), and the outer expectation is over the distribution of \(\hat\theta\).

Bias of \(\bar \ell(\hat \theta)\) as an estimator of \(\Delta\)

\[ {\mathop{\mathrm{E}}}_g\{\bar \ell(\hat \theta)\} - \Delta = \underbrace{{\mathop{\mathrm{E}}}_g\{\bar \ell(\hat \theta) - \bar \ell(\theta_g)\}}_{a} + \underbrace{{\mathop{\mathrm{E}}}_g\{\bar \ell(\theta_g)\} - \Delta}_{b} \]

From the asymptotic distribution of \(W(\theta_g)\) \[ \begin{aligned} a & = {\mathop{\mathrm{E}}}_g\{\bar\ell(\hat\theta) - \bar\ell(\theta_g)\} \\ & = \frac{1}{2n}E_g\{W(\theta_g)\} \\ & \approx \frac{1}{2n}\mathop{\mathrm{tr}}\{I(\theta_g)^{-1} K(\theta_g)\} \end{aligned} \]

A Taylor expansion of \(\bar\ell^+(\hat\theta)\) around \(\theta_g\) and results on inference under the wrong model can be used to show that \[ \begin{aligned} b & = {\mathop{\mathrm{E}}}_g\{\bar \ell(\theta_g)\} - \Delta \\ & \approx \frac{1}{2n} \mathop{\mathrm{tr}}\{I(\theta_g)^{-1} K(\theta_g)\} \end{aligned} \]

\[\LARGE\Downarrow\]

\[ {\mathop{\mathrm{E}}}_g\{\bar \ell(\hat \theta)\} - \Delta \approx \frac{1}{n} \mathop{\mathrm{tr}}\{I(\theta_g)^{-1} K(\theta_g)\} \]

Takeuchi information criterion

We can correct the bias of \(\bar\ell(\hat\theta)\) as an estimator \(\Delta\), by maximizing \[ \bar\ell(\hat\theta) - \frac{1}{n}\mathop{\mathrm{tr}}(\hat J^{-1} \hat K) \] over the candidate models.

Equivalent formulations

Maximize \[ \hat \ell - \mathop{\mathrm{tr}}(\hat J^{-1} \hat K) \]

Minimize \[ 2\{\mathop{\mathrm{tr}}(\hat J^{-1}\hat K)-\hat\ell\} \tag{3}\]

(3) is called the Takeuchi Information Criterion and has also been refereed to as the Network Information Criterion.

Information criteria

\(p\) is the number of parameters in a candidate model and \(\hat\ell\) the corresponding maximized log-likelihood.

Information criterion	Acronym	Definition
Takeuchi Information Criterion	TIC	\(2\{\mathop{\mathrm{tr}}(\hat J^{-1}\hat K) - \hat\ell\}\)
Akaike Information Criterion	AIC	\(2(p - \hat\ell)\)
Corrected AIC	AIC\(_\text{c}\)	\(2(p + (p^2 + p) / (n - p - 1) - \hat\ell)\)
Bayesian Information Criterion	BIC	\(2(p \log n / 2 - \hat\ell)\)
Deviance Information Criterion	DIC
Extended Information Criterion	EIC
Generalized Information Criterion	GIC
	\(\vdots\)

A popular model selection criterion in regression problems is Mallows’ \(C_p = \text{RSS}/s^2 + 2p-n\), where \(s^2\) is an estimate of the error variance \(\sigma^2\).

Nodal involvement: AIC

mods_AIC <- dredge(nodal_full, rank = AIC)
head(mods_AIC, 10)

Global model call: glm(formula = r ~ aged + stage + grade + xray + acid, family = "binomial", 
    data = nodal, na.action = "na.fail")
---
Model selection table 
   (Intrc) acid aged grade stage xray df  logLik  AIC delta weight
26  -3.052    +                +    +  4 -24.590 57.2  0.00  0.268
30  -3.262    +          +     +    +  5 -23.880 57.8  0.58  0.201
28  -2.778    +    +           +    +  5 -24.380 58.8  1.58  0.122
22  -2.734    +          +          +  4 -25.409 58.8  1.64  0.118
32  -3.079    +    +     +     +    +  6 -23.805 59.6  2.43  0.080
25  -2.082                     +    +  3 -27.231 60.5  3.28  0.052
18  -2.176    +                     +  3 -27.394 60.8  3.61  0.044
24  -2.687    +    +     +          +  5 -25.404 60.8  3.63  0.044
14  -2.894    +          +     +       4 -26.581 61.2  3.98  0.037
27  -1.735         +           +    +  4 -26.606 61.2  4.03  0.036
Models ranked by AIC(x) 

Nodal involvement: BIC

mods_BIC <- dredge(nodal_full, rank = BIC)
head(mods_BIC, 10)

Global model call: glm(formula = r ~ aged + stage + grade + xray + acid, family = "binomial", 
    data = nodal, na.action = "na.fail")
---
Model selection table 
   (Intrc) acid aged grade stage xray df  logLik  BIC delta weight
26  -3.052    +                +    +  4 -24.590 65.1  0.00  0.278
25  -2.082                     +    +  3 -27.231 66.4  1.31  0.144
22  -2.734    +          +          +  4 -25.409 66.7  1.64  0.123
18  -2.176    +                     +  3 -27.394 66.7  1.64  0.123
30  -3.262    +          +     +    +  5 -23.880 67.6  2.55  0.078
10  -2.509    +                +       3 -27.957 67.8  2.76  0.070
6   -2.418    +          +             3 -28.131 68.2  3.11  0.059
28  -2.778    +    +           +    +  5 -24.380 68.6  3.55  0.047
17  -1.135                          +  2 -30.465 68.9  3.81  0.041
14  -2.894    +          +     +       4 -26.581 69.0  3.98  0.038
Models ranked by BIC(x) 

Nodal involvement: AIC, BIC

par(mfrow = c(1, 2))
plot(AIC ~ df, data = mods_AIC, xlab = "Number of parameters",
     bg = "#ff7518", pch = 21)
plot(BIC ~ df, data = mods_BIC, xlab = "Number of parameters",
     bg = "#ff7518", pch = 21)

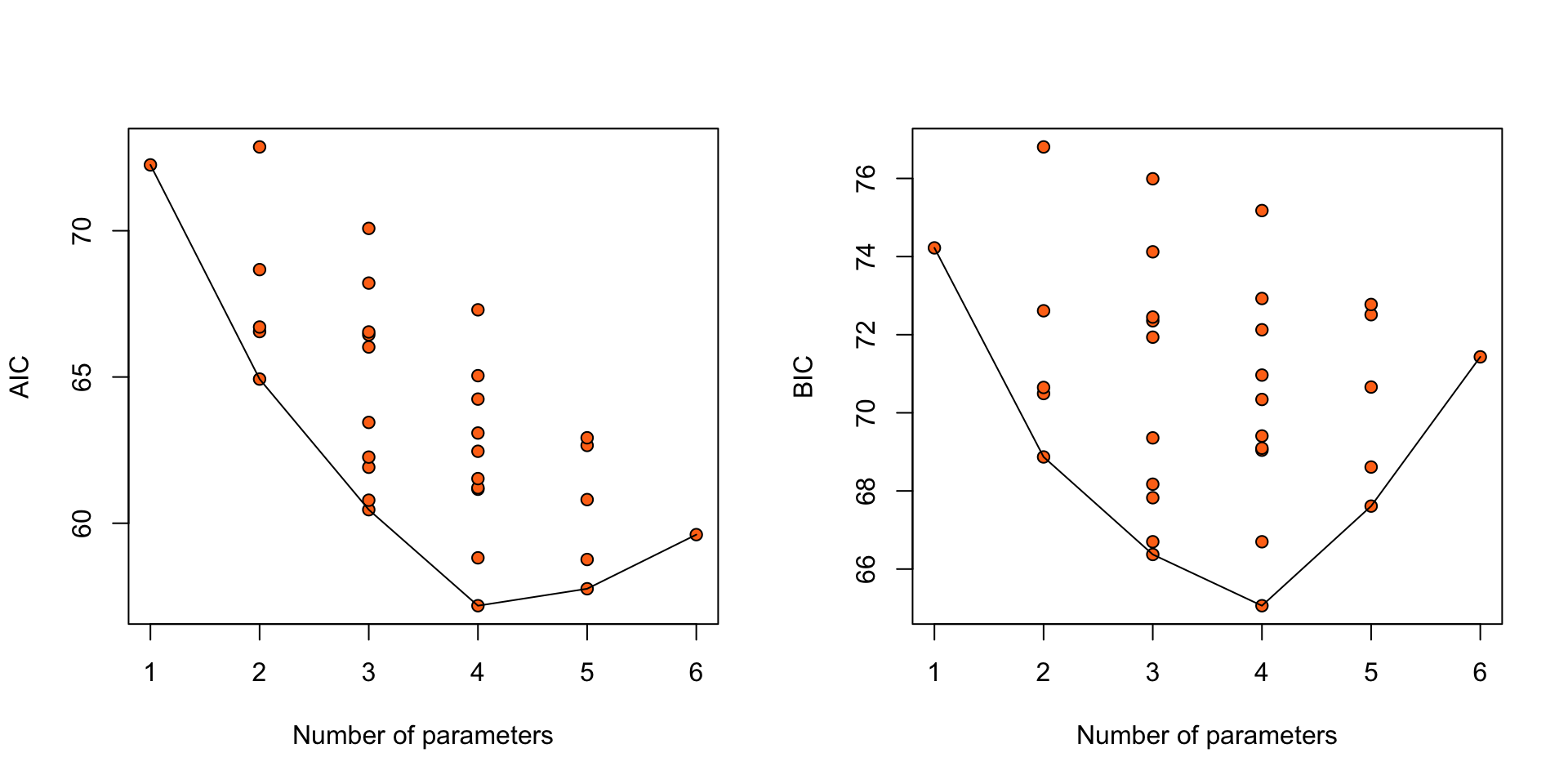
Figure 2: AIC and BIC for 32 logistic regression models for the nodal data.

Properties of model selection procedures

Asymptotic efficiency

Suppose the true model is of infinite dimensions. A model selection procedure that selects the candidate “closest” to the true model for large \(n\) is called asymptotically efficient.

Consistency

Suppose that the true model is among the candidate models. A model selection procedure that selects the true model with probability tending to one as \(n\to\infty\) is called consistent.

Asymptotic analysis of AIC, BIC, TIC

Let \(\text{IC} = c(n, p) - 2\hat\ell\) be an information criterion for a candidate model, and IC\(_+\) be the value of the information criterion for a model with one extra parameter.

\[ \begin{aligned} P(\text{IC}_+ < \text{IC}) &= P\left\{ c(n,p+1)-2\hat\ell_+< c(n,p)-2\hat\ell\right\} \\ & = P\left\{2(\hat\ell_+ - \hat\ell) > d(n, p) \right\} \end{aligned} \]

Table 1: Difference in IC penalties

Criterion	\(d(n, p)\)
AIC	\(= 2\)
TIC	\(\approx 2\) for large \(n\)
BIC	\(= \log n\)

\(2(\hat\ell_+-\hat\ell)\) converges in distribution to a \(\chi^2_1\) random variable. So, as \(n\to\infty\), \[ P(\text{IC}_+<\text{IC}) \to \begin{cases} 0.157, & \text{if AIC or TIC is used} \\ 0, & \text{if BIC is used} \end{cases} \]

Linear models

Variable selection for linear models

Model

\(Y = X^*\beta + \epsilon\)

\(\mathop{\mathrm{E}}(\epsilon) = 0\), \(\mathop{\mathrm{cov}}(\epsilon) = \sigma^2 I_n\)

\(X^*\) is an \(n \times p^*\) matrix with rows \(x_1^*, \ldots, x_n^*\) and \(j\)th column \(v_j\), \(j \in \mathcal{I}= \{1, \ldots, p^*\}\)

Data generating process

\(Y = X^\dagger \beta^\dagger + \epsilon\)

\(X^\dagger\) is an \(n \times p_0\) matrix with columns \(\{v_j : j \in \mathcal{J}\subseteq \mathcal{I}\}\), \(|\mathcal{J}| = p_0 \le p^*\)

Aim

Estimate \(\mathcal{J}\) based on data

Variable selection for linear models

Column selection is variable selection

Selecting columns of \(X^*\) is equivalent to estimating the sets \[ \mathcal{J}= \{j \in \mathcal{I}: \beta_j \ne 0\} \quad \text{and} \quad \mathcal{K}= \{j \in \mathcal{I}: \beta_j = 0\} \]

Candidate model

\(Y = X\beta + \epsilon\)

\(X\) has the columns of \(X^*\) with indices in \(\mathcal{S}\subseteq \mathcal{I}\), \(|\mathcal{S}| = p \le p^*\)

Types of selected models

Type	Selected set \(\mathcal{S}\)
Correct	\(\mathcal{J}\subseteq \mathcal{S}\subseteq \mathcal{I}\)
Wrong	\(\mathcal{S}\not\subset \mathcal{J}\)
True	\(\mathcal{J}\)

Prediction mean squared error

Fitted values from candidate model

\[ X\hat\beta = X \{ (X^\top X)^{-1}X^\top Y\} = H Y = H\mu + H\epsilon \]

\(\mu = \mathop{\mathrm{E}}(Y \mid X^*) = X^* \beta\)

\(H = X (X^\top X)^{-1} X^\top\) is the hat matrix

Prediction mean squared error

\[ \Delta = n^{-1} {\mathop{\mathrm{E}}} \left[{\mathop{\mathrm{E}}}_+\left\{ (Y_+ - X\hat\beta)^\top (Y_+ - X\hat\beta) \right\}\right] \] where expectations are taken over both \(Y\) and \(Y_+\)

\(Y_+ = \mu + \epsilon_+\) with \(\epsilon_+\) is an independent copy of \(\epsilon\)

Bias / Variance trade-off

\(Y_{+} - X\hat\beta = {\color[rgb]{1,1,1}{Y_{+} - H Y = \mu + \epsilon_{+} - H \mu - H \epsilon = (I_n - H) \mu + (\epsilon_{+} - H \epsilon)}}\)

\((Y_{+} - X\hat\beta)^\top (Y_{+} - X\hat\beta) = {\color[rgb]{1,1,1}{\mu (I_n - H) \mu + \epsilon_{+}^\top \epsilon_{+} + \epsilon^\top H \epsilon + Z}}\)

where \(Z\) collects all terms with \({\mathop{\mathrm{E}}}[{\mathop{\mathrm{E}}}_{+}(Z)] = 0\). From the assumptions on the errors, we have \({\mathop{\mathrm{E}}}[{\mathop{\mathrm{E}}}_{+}(\epsilon_{+}^\top \epsilon_{+})] = n \sigma^2\), and \({\mathop{\mathrm{E}}}[{\mathop{\mathrm{E}}}_{+}(\epsilon^\top H \epsilon)] = \mathop{\mathrm{tr}}{H}\sigma^2 = p\sigma^2\). Collecting terms

Prediction mean squared error

\[ \Delta = \underbrace{\mu (I_n - H) \mu / n}_{\text{Bias}} + \overbrace{(1 + p / n) \sigma^2}^{\text{Variance}} \]

Bias / Variance trade-off

Type	Selected set \(\mathcal{S}\)	\(\Delta\)
Wrong	\(\mathcal{S}\not\subset \mathcal{J}\)	\(\mu (I_n - H) \mu / n + (1 + p / n) \sigma^2\)
Correct	\(\mathcal{J}\subseteq \mathcal{S}\subseteq \mathcal{I}\)	\((1 + p / n) \sigma^2\), \(p \ge p_0\)
True	\(\mathcal{J}\)	\((1 + p_0 / n) \sigma^2\)

Bias

\(n^{-1}\mu^\top (I_n - H) \mu = n^{-1}\|\mu - H\mu\|_2^2 \ge 0\), and zero only if the model is correct (\(H\mu = \mu\))

Bias is reduced the closer \(\mu\) is to the space spanned by the columns of \(X\)

We expect a reduction in bias when useful covariates are added to the model

Variance

\((1 + p/n) \sigma^2\) increases as \(p\) increases, for example whenever useless terms are included

Polynomial regression

True model

\[ Y_i = \sum_{j = 0}^{5} x_i^j + \epsilon_i \] \(\mu_i = \sum_{j = 0}^{5} x_i^j\) is a degree five polynomial

Candidate models

\[ Y_i = \sum_{j = 0}^{p - 1} \beta_j x_i^j + \epsilon_i \quad (i = 1, \ldots, n)\, , \]

\(x_1, \ldots, x_n\) generated from \(n\) independent \(\mathop{\mathrm{N}}(0, 1)\)

Polynomial regression

\(n = 20\) and \(\sigma^2 = 1\)

Delta <- function(p, p0, x, sigma2) {
    cols <- 0:(p - 1)
    cols0 <- 0:(p0 - 1)
    n <- length(x)
    X <- matrix(rep(x, p)^rep(cols, each = n), nrow = n)
    X0 <- matrix(rep(x, p0)^rep(cols0, each = n), nrow = n)
    mu <- rowSums(X0)
    H <- tcrossprod(qr.Q(qr(X)))
    bias <- sum(((diag(n) - H) %*% mu)^2) / n
    variance <- sigma2 * (1 + p / n)
    c(p = p, bias = bias, variance = variance)
}

n <- 20
sigma2 <- 1
p_max <- 15
set.seed(1)
x <- rnorm(n)
D <- data.frame(t(sapply(1:p_max, Delta, p0 = 6, x = x, sigma2 = 1)))

par(mfrow = c(1, 3))
plot(sqrt(bias) ~ p, data = D, subset = p > 2,
     main = expression(sqrt("Bias")), ylab = "",
     type = "b", bg = "#ff7518", pch = 21)
abline(v = 6, lty = 3, col = "grey")
plot(sqrt(variance) ~ p, data = D, subset = p > 2,
     main = expression(sqrt("Variance")), ylab = "", 
     type = "b", bg = "#ff7518", pch = 21)
abline(v = 6, lty = 3, col = "grey")
plot(sqrt(bias + variance) ~ p, data = D, subset = p > 2,
     main = expression(sqrt(Delta)), ylab = "",
     type = "b", bg = "#ff7518", pch = 21)
abline(v = 6, lty = 3, col = "grey")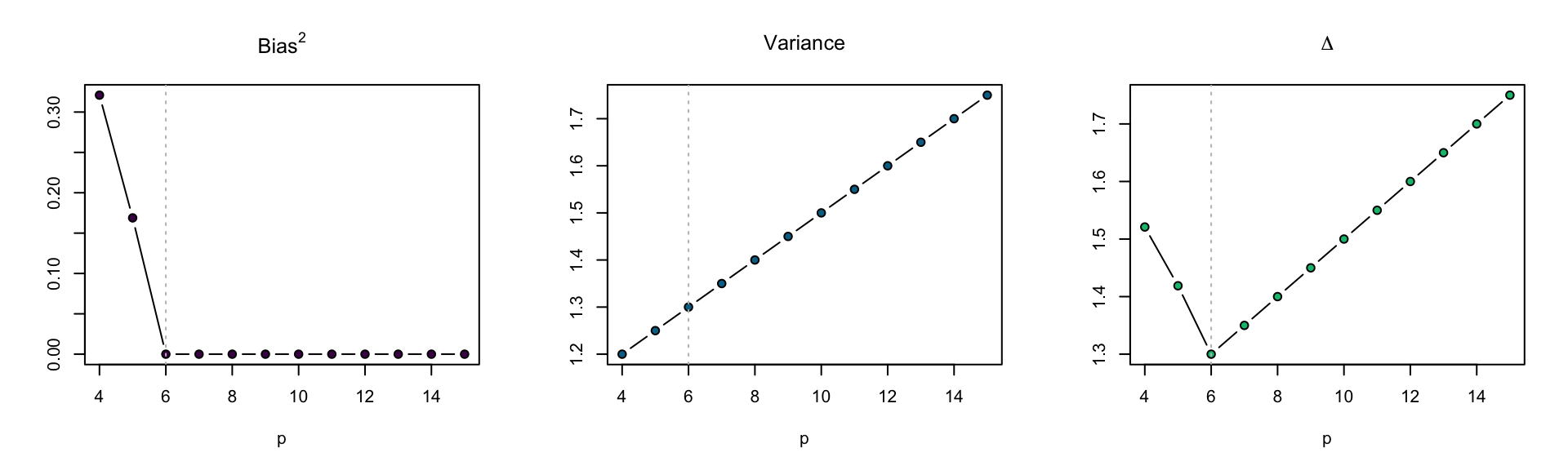

Figure 3: \(\Delta\) for models with varying polynomial degree.

Data splitting

\(\Delta\) depends on \(\mu\) and \(\sigma^2\), which are unknown. But we can use the assumption of exchangeability of \(Y_1, \ldots, Y_n\) given the covariates to estimate it.

1. For each candidate model:

   • Split data into \((X, y)\) and \((X_{+}, y_{+})\), where \(X_{+}\) is an \(n_{+} \times p\) matrix, and \(y_{+}\) is the vector of the corresponding \(n_{+}\) response values.

   • Estimate the model using \((X, y)\).

   • Compute \[ \hat\Delta = \frac{1}{n_{+}}(y_{+} - X_{+}\hat\beta)^\top (y_{+} - X_{+}\hat\beta) = \frac{1}{n_{+}}\sum_{i = 1}^{n_{+}}(y_{+, i} - x_{+, i}^\top \hat\beta)^2 \] where \(\hat\beta\) is the least squares estimator of the candidate model.

2. Choose the candidate model with the smallest \(\hat\Delta\).

Cross validation

Depending on \(n\), data splitting may not the most efficient use of the available information.

\(\Delta\) can instead be estimated using leave-one-out cross-validation as \[ \hat\Delta_\text{CV} = \frac{1}{n} \sum_{i=1}^n (y_i - x_i^\top \hat\beta_{-i})^2 \tag{4}\] where \(\hat\beta_{-j}\) is the estimate computed without the \(i\)th observation.

(4) suggests that we need \(n\) fits to compute \(\hat\Delta_\text{CV}\). But, it can be shown that \[ \hat\Delta_\text{CV} = \frac{1}{n} \sum_{i=1}^n \frac{(y_i - x_i^\top \hat\beta)^2}{(1 - h_{ii})^2} \] where \(h_{11},\ldots, h_{nn}\) are diagonal elements of \(H\).

Generalized cross validation

Another estimator of \(\Delta\) uses generalized cross-validation and has the form \[ \hat\Delta_\text{GCV} = \frac{1}{n} \sum_{i = 1}^n \frac{(y_i - x_i^\top \hat\beta)^2}{\{1 - \mathop{\mathrm{tr}}(H)/n\}^2} \]

It holds that \[ \mathop{\mathrm{E}}(\hat \Delta_\text{GCV}) = \frac{1}{n(1 - p / n)^2} \mu^\top (I_n - H)\mu + \frac{1}{1 - p / n} \sigma^2 \, . \] For large \(n\), \(\mathop{\mathrm{E}}(\hat \Delta_\text{GCV}) \approx \Delta\).

Generalized cross validation

Proof. It holds that \(Y - X\hat\beta = (I_n - H) Y = (I_n - H) \mu + (I_n - H) \epsilon\). So, \[ (Y - X\hat\beta)^\top (Y - X\hat\beta) = {\color[rgb]{1,1,1}{\mu^\top (I_n - H) \mu + \epsilon^\top (I_n - H) \epsilon + Z}} \] where the terms collected in \(Z\) have expectation zero. Using the fact that \(\mathop{\mathrm{tr}}{H} = p\), \[ \begin{aligned} \mathop{\mathrm{E}}(\hat \Delta_\text{GCV}) & = {\color[rgb]{1,1,1}{\frac{1}{n(1 - p / n)^2}\mu^\top (I_n - H) \mu + \frac{(n - p)}{n(1 - p / n)^2} \sigma^2}} \\ & = {\color[rgb]{1,1,1}{\frac{1}{n(1 - p / n)^2} \mu^\top (I_n - H) \mu + \frac{1}{1 - p/n}\sigma^2}} \end{aligned} \tag{5}\]

For large \(n\) or small \(z = 1 / n\), a Taylor expansion of \((1 - p z)^{-1}\) about \(z = 0\) gives \((1 - p z)^{-1} = {\color[rgb]{1,1,1}{1 + p z + O(z^2)}}\). Also, \(z (1 - z p)^{-2} = {\color[rgb]{1,1,1}{z + O(z^2)}}\). Replacing \((1 - p/n)^{-1}\) and \(n^{-1}(1 - p / n)^{-2}\) in the last expression in (5) with their first order approximations gives \[ \Delta = \mu (I_n - H) \mu / n + (1 + p / n) \sigma^2 \]

Bayesian model selection

Thomas Bayes (1701 - 1761)

\[ P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)} \]

in Bayes (1763/4). Essay towards solving a problem in the doctrine of chances. Philosophical Transactions of the Royal Society of London.

Most likely not Thomas Bayes’ portrait.

Bayesian inference

Frequentist viewpoint (cartoon version)

• There is a quantity \(\theta\) that characterizes aspects of how the data is generated and is treated as an unknown constant.

• Probability statements concern randomness in hypothetical replications of the data (possibly conditioned on an ancillary statistic).

Bayesian viewpoint (cartoon version)

• All ignorance should be expressed in terms of probability statements.

• A joint probability distribution for data and all unknowns can be constructed.

• Bayes’ theorem is used to convert prior beliefs \(\pi(\theta)\) about unknown \(\theta\) into posterior beliefs \(\pi(\theta\mid y)\), conditioned on data.

• Probability statements concern randomness of unknowns, conditioned on all known quantities.

A joke by Xiao-Li Meng

Bayesian updating

Data \[ y \]

Likelihood (summarizes modelling assumptions / experimental conditions) \[ f(y \mid \theta), \quad \text{where} \quad \theta\in\Omega_\theta \]

Prior distribution (summarizes prior information about \(\theta\)) \[ \pi(\theta) \]

Posterior distribution (summarizes information about \(\theta\), conditional on the observed data \(y\)) \[ \pi(\theta\mid y ) = \frac{\pi(\theta) f(y\mid\theta)}{\int \pi(\theta) f(y\mid\theta)\, d\theta} \]

Marginal posterior

If \(\theta = (\psi^\top,\lambda^\top)^\top\), then inference for \(\psi\) is based on the marginal posterior \[ \pi(\psi\mid y) = \int \pi(\theta\mid y )\, d\lambda \]

Bayesian model selection

\(M\) alternative models for the data, with respective parameters \(\theta_1 \in \Omega_{\theta_1}, \ldots, \theta_M \in \Omega_{\theta_M}\)

Parameter space

\[ \theta \in \Omega = \bigcup_{m=1}^M \{m\}\times \Omega_{\theta_m} \]

Prior distributions for model parameters

\[ \pi_m(\theta_m \mid m) \]

Prior probabilities for models

\[ \pi(m) \]

Prior information for each model

\[ \pi(m, \theta_m) = \pi(\theta_m \mid m)\pi(m) \]

Inference about model choice

Marginal posterior probability mass function

\[ \begin{aligned} \pi(m\mid y) = \frac{\int f(y\mid\theta_m)\pi_m(\theta_m)\pi(m)\, d\theta_m} {\sum_{m'=1}^M \int f(y\mid\theta_{m'})\pi_{m'}(\theta_{m'})\pi(m')\, d\theta_{m'}} = \frac{\pi(m) \overbrace{f(y\mid m)}^{\text{marginal likelihood}}} {\sum_{m'=1}^M \pi(m') f(y\mid{m'})} \end{aligned} \]

Inference about models and parameters

Joint posterior of model and parameters

\[ \pi(m, \theta_m \mid y) =\pi(\theta_m \mid m, y)\pi(m \mid y) \]

Bayesian updating

\[ \pi(\theta_m\mid m)\pi(m) \mapsto \pi(\theta_m \mid m, y) \pi(m\mid y) \]

For each model \(m \in \{1,\ldots, M\}\), it is necessary to compute

• \(\pi(m \mid y)\), which involves \(f(y\mid m) = \int f(y\mid\theta_m,m)\pi(\theta_m\mid m)\, d\theta_m\)

• \(\pi(\theta_m \mid y, m)\)

Posterior odds = Prior odds \(\times\) Bayes factor

If there are just two models, we can write \[ \underbrace{\frac{\pi(1\mid y)}{\pi(2\mid y)}}_{\text{Posterior odds}} = \overbrace{\frac{\pi(1)}{\pi(2)}}^{\text{Prior odds}} \underbrace{\frac{f(y\mid 1)}{f(y\mid 2)}}_{\text{Bayes factor}} \]

Lindsey’s paradox

Suppose that \(\theta_m\) has as \(N(0, \sigma^2 I_{p_m})\) prior, where \(\sigma^2\) is large (prior is diffuse). Then, \[ \begin{aligned} f(y \mid m) &= \sigma^{-p_m} (2\pi)^{-p_m/2} \int f(y \mid m, \theta_m) \prod_{r = 1}^{p_m} \exp \left\{-{\theta_{m,r}^2/(2\sigma^2)}\right\} d\theta_{m, r}\\ & \approx \sigma^{-p_m} (2\pi)^{-p_m/2} \int f(y \mid m, \theta_m) \prod_{r = 1}^{p_m} d\theta_{m, r} \end{aligned} \]

The Bayes factor for comparing two models is \[ \frac{f(y\mid 1)}{f(y\mid 2)}\approx \sigma^{p_2 - p_1} g(y) \] where \(g(y)\) depends on the two likelihoods but is independent of \(\sigma^2\).

\[\LARGE\Downarrow\]

Irrespective of what the data tell us about the relative merits of the two models, the Bayes factor in favour of the simpler model can be made arbitrarily large by increasing \(\sigma\).

Model averaging

If a quantity \(Z\) has the same interpretation for all models, it is desirable to allow for model uncertainty when constructing inferences or making predictions about it.

Predictive distribution of \(Z\)

\[ f(z\mid y) = \sum_{m=1}^M f(z\mid m, y) \pi(m \mid y) \]

\(Z\) is a future value

Each model may be just a vehicle that provides a future value, and not of interest on its own.

\(Z\) is a physical parameter (e.g. means, variances, etc.)

Care is needed with prior choice and ensuring that \(Z\) has the same interpretation across models.

Materials	Link
Preliminary material	ikosmidis.com/files/APTS-SM-Preliminary
Notes	ikosmidis.com/files/APTS-SM-Notes
Slides: Introduction	ikosmidis.com/files/APTS-SM-Slides-intro
Slides: Model selection	ikosmidis.com/files/APTS-SM-Slides-model-selection
Slides: Beyond GLMs	ikosmidis.com/files/APTS-SM-Slides-beyond-glms
Slides: Nonlinear models	ikosmidis.com/files/APTS-SM-Slides-nonlinear-models
Slides: Latent variables	ikosmidis.com/files/APTS-SM-Slides-latent
Lab 1	ikosmidis.com/files/APTS-SM-Notes/lab1.html
Lab 2	ikosmidis.com/files/APTS-SM-Notes/lab2.html