APTS Statistical Modelling
Nonliner models
Professor of Statistics
Department of Statistics, University of Warwick
ioannis.kosmidis@warwick.ac.uk
ikosmidis.com ikosmidis ikosmidis_
19 April 2024
Nonlinear models with fixed effects
Nonlinear predictor
Linear model
\[ Y_i = x_i^\top \beta + \epsilon_i \,, \quad \epsilon_i \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0, \sigma^2) \]
- Parameters enter the model through a linear combination of coefficients and covariates.
Nonlinear model
\[ Y_i = \eta(x_i, \beta) + \epsilon_i \,, \quad \epsilon_i \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0, \sigma^2) \]
Parameters and covariates are allowed to have a nonlinear relationship.
The linear model results for \(\eta(x_i, \beta) = x_i^\top \beta\).
Nonlinear models
Parameter types in nonlinear models
Physical parameters that have particular meaning in the subject-area where the model comes from. Estimating the value of physical parameters, then, contributes to scientific understanding.
Tuning parameters that do not necessarily have any physical meaning. Their presence is justified as a simplification of a more complex underlying system. The aim when estimating them is to make the model represent reality as well as possible.
Specification of the nonlinear predictor
Mechanistically: prior scientific knowledge is incorporated into building a mathematical model for the mean response. That model can often be complex and \(\eta(x, \beta)\) may not be available in closed form.
Phenomenologically (empirically): a function \(\eta(x, \beta)\) may be posited that appears to capture the non-linear nature of the mean response.
Calcium uptake: ?SMPracticals::calcium
The uptake of calcium (in nmoles per mg) at set times (in minutes) by \(27\) cells in “hot” suspension.
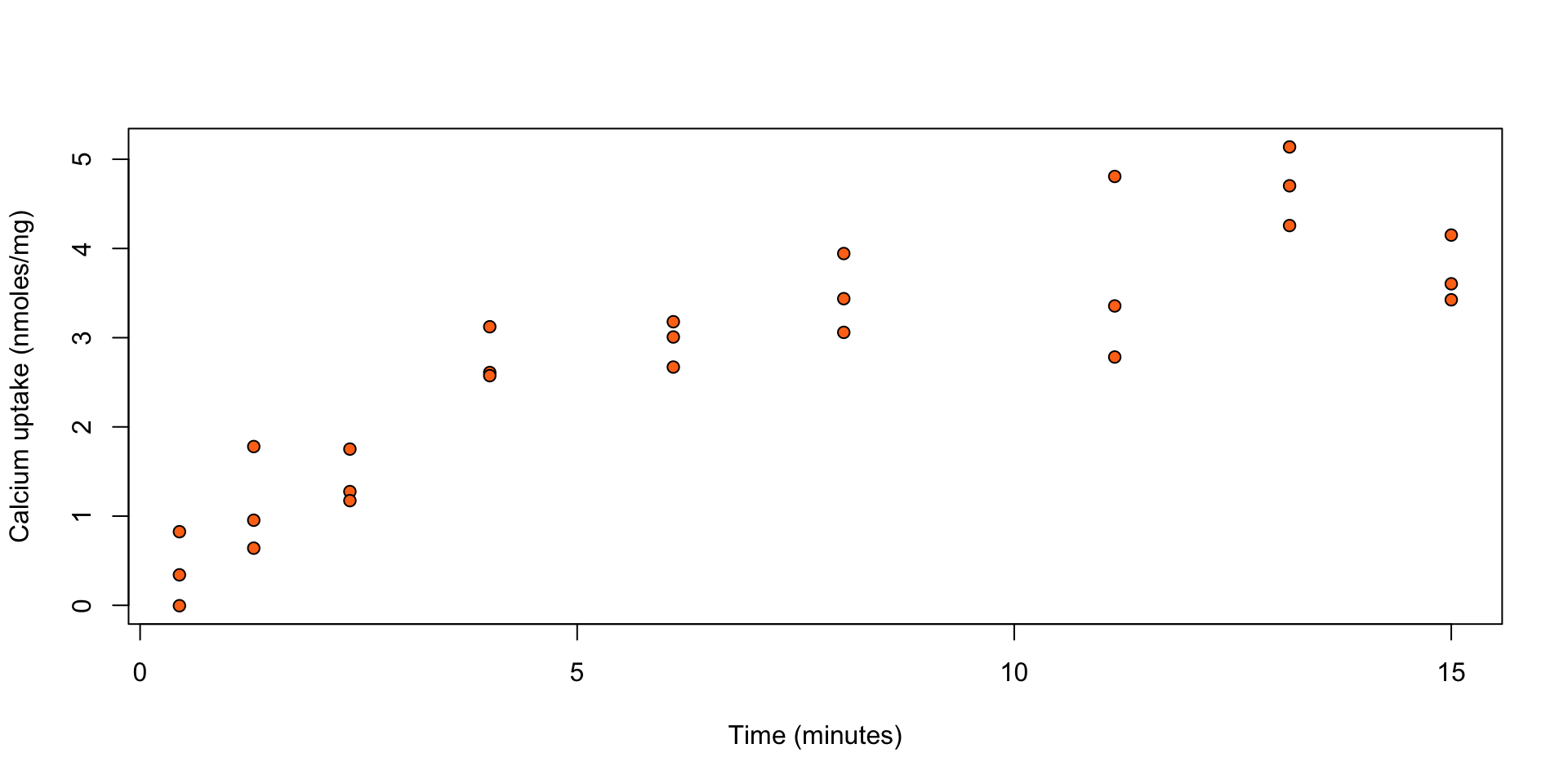
Figure 1: Calcium uptake against time.
Calcium uptake
A phenomenological model for growth curves
Assume that the rate of growth is proportional to the calcium remaining, i.e. \[ \frac{d \eta}{d t} = (\beta_0 - \eta) / \beta_1 \tag{1}\]
Solving the differential equation (1) with initial condition \(\eta(0,\beta) = 0\), gives \[ \eta(t, \beta) = \beta_0 \left( 1 - \exp \left( - t / \beta_1 \right) \right) \]
Parameter interpretation
\(\beta_0\) is the calcium uptake after infinite time.
\(\beta_1\) controls the growth rate of calcium uptake.
Calcium uptake
calc_lm1 <- lm(cal ~ time, data = calcium)
calc_lm2 <- lm(cal ~ time + I(time^2), data = calcium)
calc_nlm <- nls(cal~ beta0 * ( 1 - exp(-time/beta1)), data = calcium,
start = list(beta0 = 5, beta1 = 5))
newdata <- data.frame(time = seq(min(calcium$time), max(calcium$time), length.out = 100))
pred_lm1 <- predict(calc_lm1, newdata = newdata)
pred_lm2 <- predict(calc_lm2, newdata = newdata)
pred_nlm <- predict(calc_nlm, newdata = newdata)
plot(cal ~ time, data = calcium,
xlab = "Time (minutes)",
ylab = "Calcium uptake (nmoles/mg)",
bg = "#ff7518", pch = 21)
lines(newdata$time, pred_lm1, col = gray(0.8), lty = 1, lwd = 2)
lines(newdata$time, pred_lm2, col = gray(0.6), lty = 2, lwd = 2)
lines(newdata$time, pred_nlm, col = gray(0.4), lty = 3, lwd = 2)
legend("bottomright", legend = c("LM (linear)", "LM (quadratic)", "NLM"),
col = gray(c(0.8, 0.6, 0.4)), lty = 1:3, lwd = 2)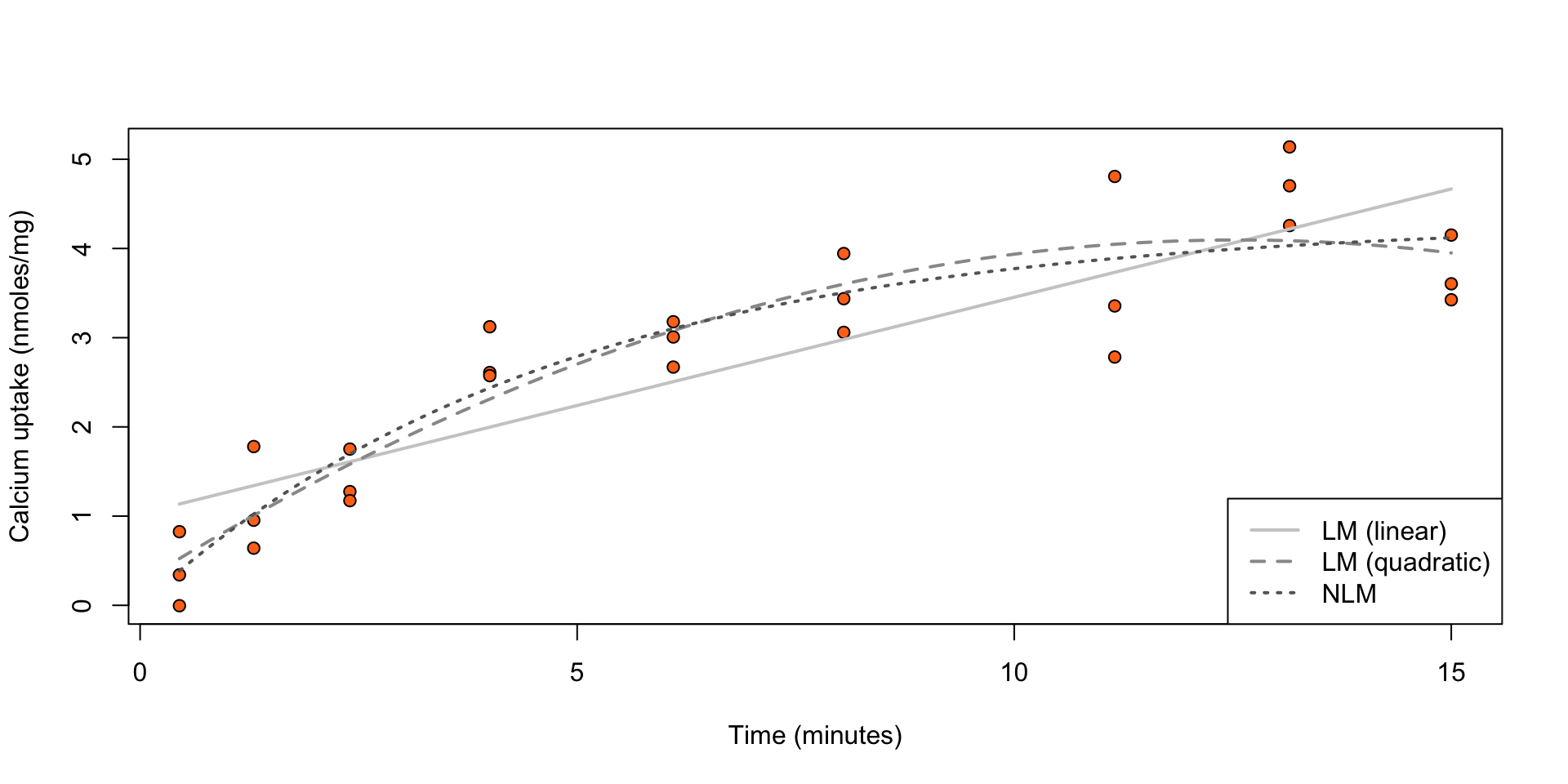
Figure 2: Calcium uptake against time, overlaid by estimated expected uptake from three models with \(\eta(t, \beta) = \beta_1 + \beta_2 t\) (LM (linear)), \(\eta(t, \beta) = \beta_1 + \beta_2 x + \beta_3 t^2\) (LM (quadratic)), \(\eta(t, \beta) = \beta_0 ( 1 - \exp ( - t / \beta_1 ))\) (NLM).
Calcium uptake
A comparison of the three models in terms of number of parameters, maximized log-likelihood value, and AIC and BIC returns
p loglik AIC BIC
LM (linear) 2 -28.701 63.403 67.290
LM (quadratic) 3 -20.955 49.910 55.093
NLM 2 -20.955 47.909 51.797Nonlinear mixed effects models
Theophylline data
data("Theoph", package = "datasets")
plot(conc ~ Time, data = Theoph, type = "n",
ylab = "Concentration (mg/L)", xlab = "Time (hours)")
for (i in 1:30) {
dat_i <- subset(Theoph, Subject == i)
lines(conc ~ Time, data = dat_i, col = "grey")
}
points(conc ~ Time, data = Theoph,
bg = "#ff7518", pch = 21, col = "grey")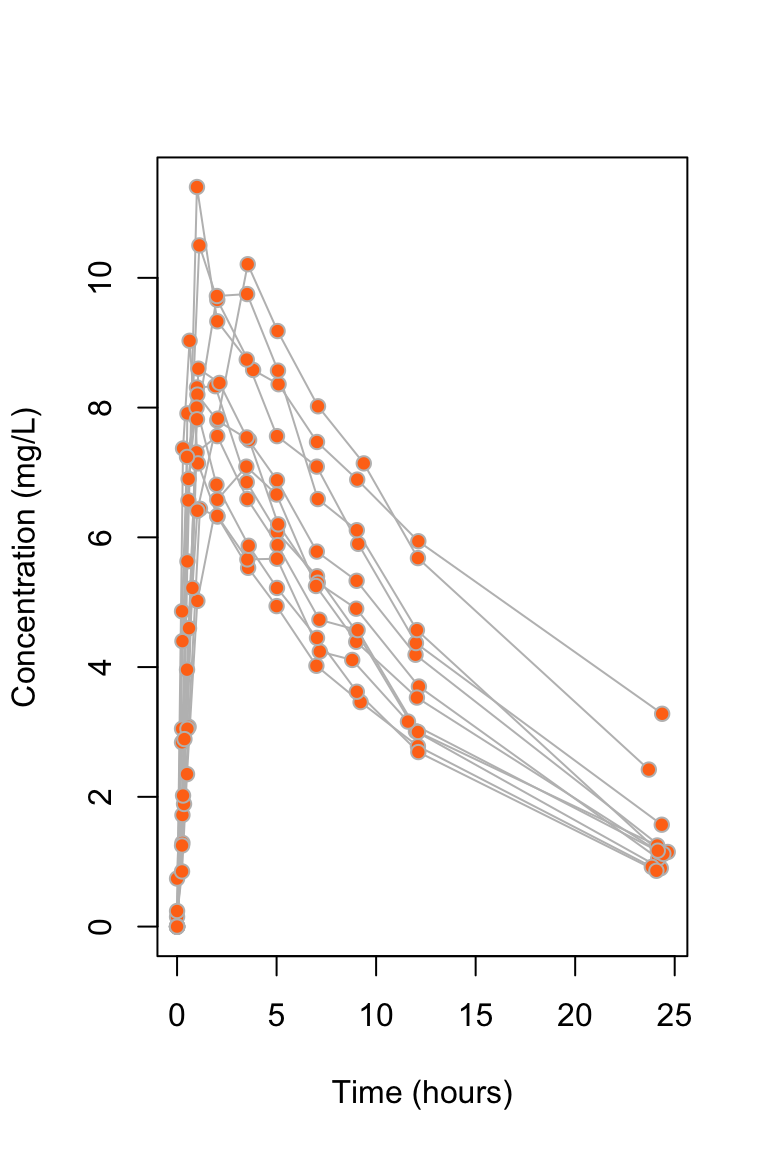
Theophylline is an anti-asthmatic drug. An experiment was performed on \(12\) individuals to investigate the way in which the drug leaves the body. The study of drug concentrations inside organisms is called pharmacokinetics.
An oral dose was given to each individual at time \(t = 0\), and the concentration of theophylline in the blood was then measured at 11 time points in the next 25 hours.
Theophylline data: Compartmental models
Compartmental models are a common class of model used in pharmacokinetics studies.
If the initial dosage is \(D\), then pharmacokinetic model with a first-order compartment function is \[ \eta(\beta, D,t) = \frac{D \beta_1 \beta_2}{\beta_3(\beta_2 - \beta_1)} \left( \exp \left( - \beta_1 t\right) - \exp \left( - \beta_2 t\right)\right)\ \tag{2}\] where
\(\beta_1 > 0\): the elimination rate which controls the rate at which the drug leaves the organism.
\(\beta_2 > 0\): the absorption rate which controls the rate at which the drug enters the blood.
\(\beta_3 > 0\): the clearance which controls the volume of blood for which a drug is completely removed per time unit.
Theophylline data: Compartmental models
Since all the parameters are positive, and their estimation will most probably require a gradient descent step (e.g. what some of the methods in optim do), it is best to rewrite (2) in terms of \(\gamma_i = log(\beta_i)\). We can write \[
\eta'(\gamma, D, t) = \eta(\beta, D, t) = D \frac{\exp(-\exp(\gamma_1) t) - \exp(-\exp(\gamma_2) t)}{\exp(\gamma_3 - \gamma_1) - \exp(\gamma_3 - \gamma_2)}
\] where
\(\gamma_1 \in \Re\): the logarithm of the elimination rate.
\(\gamma_2 \in \Re\): the logarithm of the absorption rate.
\(\gamma_3 \in \Re\): the logarithm of the clearance.
Theophylline data: Fitting a pharmacokinetic model
We fit the model with predictor \(\eta'(\gamma, D_i,t_{ij})\) using nonlinear least-squares (nls() in R).
Formula: conc ~ Dose * (exp(-exp(gamma1) * Time) - exp(-exp(gamma2) *
Time))/(exp(gamma3 - gamma1) - exp(gamma3 - gamma2))
Parameters:
Estimate Std. Error t value Pr(>|t|)
gamma1 0.39922 0.11754 3.397 0.000908 ***
gamma2 -2.52424 0.11035 -22.875 < 2e-16 ***
gamma3 -3.24826 0.07439 -43.663 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.459 on 129 degrees of freedom
Number of iterations to convergence: 8
Achieved convergence tolerance: 3.709e-06The estimates and estimated standard errors (using the delta method) for \(\beta_1\), \(\beta_2\) and \(\beta_3\) are
Theophylline data: Fit assessment
res <- residuals(pkm, type = "pearson")
ord <- order(ave(res, Theoph$Subject))
subj <- Theoph$Subject[ord]
subj <- factor(subj, levels = unique(subj), ordered = TRUE)
plot(res[ord] ~ subj,
xlab = "Subject (ordered by mean residual)",
ylab = "Pearson residual",
col = "#ff7518", pch = 21)
abline(h = 0, lty = 2)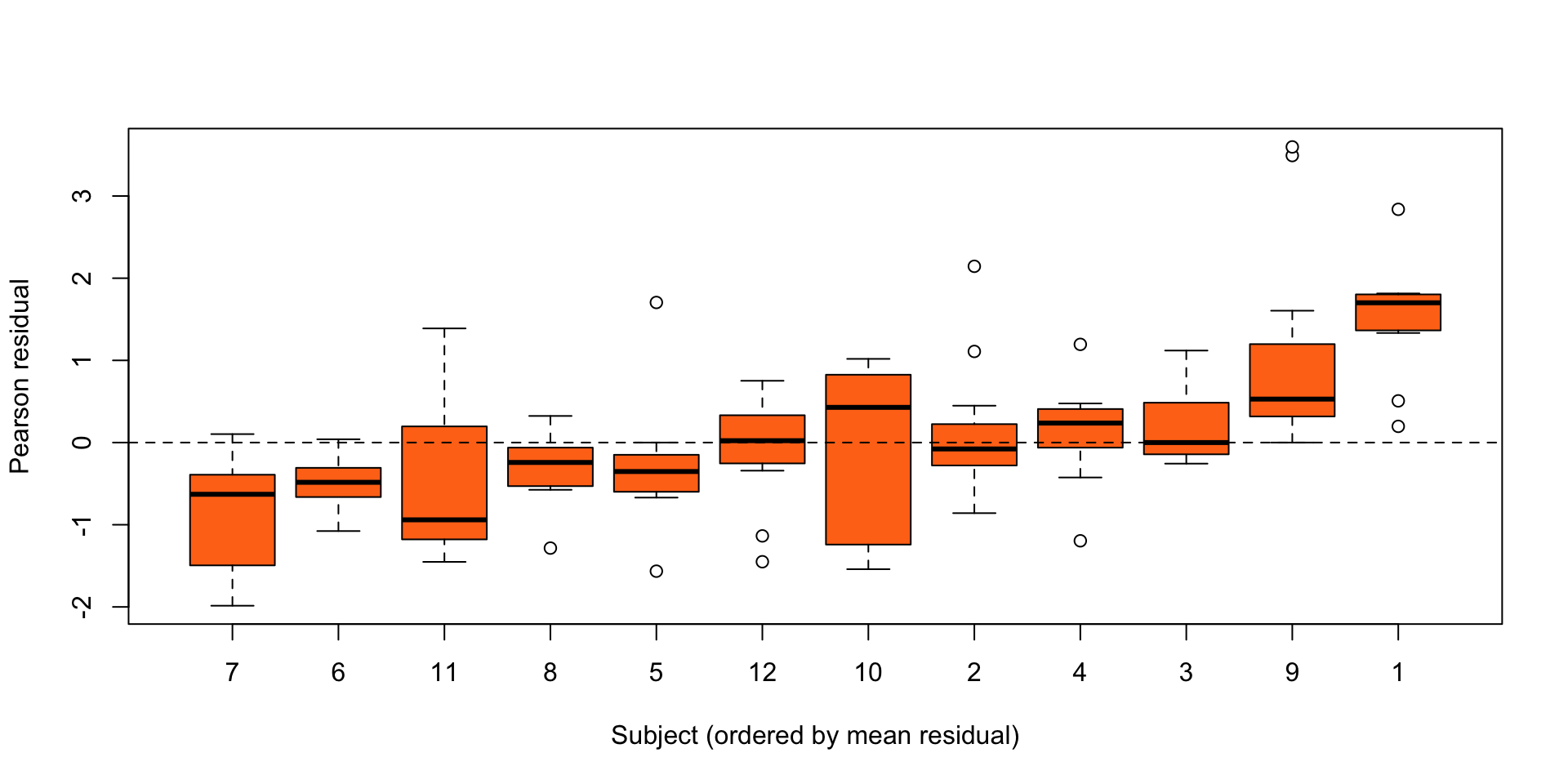
Figure 4: Residuals for each individual in the theopylline study from the nonlinear model \(Y_{ij} = \eta'(\gamma, D_i,t_{ij}) + \epsilon_{ij}\), \(\epsilon_{ij} \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0,\sigma^2)\).
Clear evidence of unexplained differences between individuals.
Theophylline data: Fit assessment
library("ggplot2")
st <- unique(Theoph[c("Subject", "Dose")])
pred_df <- as.list(rep(NA, nrow(st)))
for (i in seq.int(nrow(st))) {
pred_df[[i]] <- data.frame(Time = seq(0, 25, by = 0.2),
Dose = st$Dose[i],
Subject = st$Subject[i])
}
pred_df <- do.call("rbind", pred_df)
pred_df$conc <- predict(pkm, newdata = pred_df)
## Order according to mean residual
theoph <- within(Theoph, Subject <- factor(Subject, levels = unique(subj), ordered = TRUE))
fig_theoph <- ggplot(theoph) +
geom_point(aes(Time, conc), col = "#ff7518") +
geom_hline(aes(yintercept = Dose), col = "grey", lty = 3) +
facet_wrap(~ Subject, ncol = 3) +
labs(y = "Concentration (mg/L)", x = "Time (hours)") +
theme_bw()
fig_theoph +
geom_line(data = pred_df, aes(Time, conc), col = "grey") 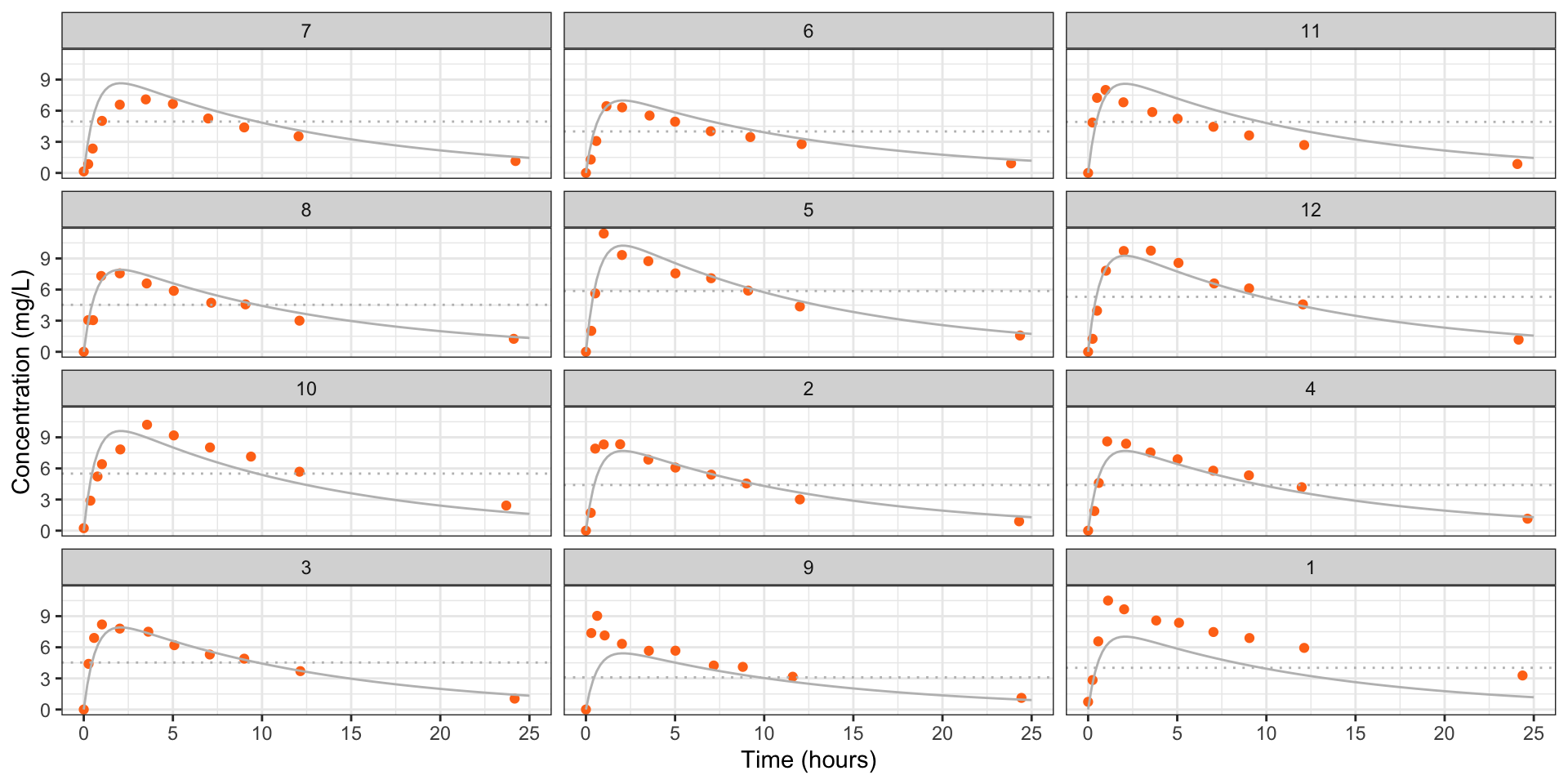
Figure 5: Estimated concentrations (grey) for each individual in the theopylline study from the nonlinear model \(Y_{ij} = \eta'(\gamma, D_i,t_{ij}) + \epsilon_{ij}\), \(\epsilon_{ij} \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0,\sigma^2)\). The dotted line is the administered dose.
Accounting for heterogeneity between individuals seems worthwhile.
Nonlinear mixed effects models
\[ Y_{ij} = \eta(\beta + A b_i, x_{ij}) + \epsilon_{ij} \,, \quad \epsilon_{ij} \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0,\sigma^2)\,, \quad b_i \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0,\Sigma_b) \] where \(\Sigma_b\) is a \(q \times q\) covariance matrix and \(A\) is a \(p \times q\) matrix of zeros and ones, which determines which parameters are fixed and which are varying.
The linear mixed model is a special case of the nonlinear mixed model with \[ \eta(\beta + A b_i, x_{ij}) = x_{ij}^\top \left( \beta + A b_i\right) = x_{ij}^\top \beta + x_{ij}^\top A b_i = x_{ij}^\top \beta + z_{ij}^\top b_i \,. \]
A random intercept model results, if the first element of \(x_{ij}\) is \(1\) for all \(i\) and \(j\), \(q = 1\) and \(A = (1, 0, \ldots, 0)^\top\).
Theophylline data
We fit a nonlinear mixed model that allows all the parameters to vary across individuals, i.e. \(A = I_3\) using nmle() from the nlme R package.
Nonlinear mixed-effects model fit by maximum likelihood
Model: fm
Data: Theoph
Log-likelihood: -173.32
Fixed: gamma1 + gamma2 + gamma3 ~ 1
gamma1 gamma2 gamma3
0.4514513 -2.4326850 -3.2144578
Random effects:
Formula: list(gamma1 ~ 1, gamma2 ~ 1, gamma3 ~ 1)
Level: Subject
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
gamma1 0.6376932 gamma1 gamma2
gamma2 0.1310518 0.012
gamma3 0.2511873 -0.089 0.995
Residual 0.6818359
Number of Observations: 132
Number of Groups: 12 Theophylline data
We fit a nonlinear mixed model that allows all the parameters to vary across individuals, i.e. \(A = I_3\) using nmle() from the nlme R package.
Nonlinear mixed-effects model fit by maximum likelihood
Model: fm
Data: Theoph
Log-likelihood: -173.32
Fixed: gamma1 + gamma2 + gamma3 ~ 1
gamma1 gamma2 gamma3
0.4514513 -2.4326850 -3.2144578
Random effects:
Formula: list(gamma1 ~ 1, gamma2 ~ 1, gamma3 ~ 1)
Level: Subject
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
gamma1 0.6376932 gamma1 gamma2
gamma2 0.1310518 0.012
gamma3 0.2511873 -0.089 0.995
Residual 0.6818359
Number of Observations: 132
Number of Groups: 12 Theophylline data
Let’s consider the model with random effects with means \(\gamma_1\) and \(\gamma_3\), and just a population parameter for the logarithm of the absorption rate.
\[ Y_{ij} = \eta'\left( \begin{bmatrix} \gamma_1 + b_{i1} \\ \gamma_2 \\ \gamma_3 + b_{i3} \end{bmatrix}, D_i, t_{ij}\right) + \epsilon_{ij} \, \quad \epsilon_{ij} \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0,\sigma^2)\,, \quad (b_{i1}, b_{i3})^\top \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0,\Sigma_b) \] This corresponds to the general form pf the nonlinear mixed effects model with \[ A = \begin{bmatrix} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{bmatrix} \quad \text{and} \quad b_i = \begin{bmatrix} b_{i1} \\ b_{i3} \end{bmatrix} \]
A comparison to the model with all effects varying across individuals gives
Theophylline data
conc_nlm <- pred_df$conc
conc_nlme_2 <- predict(pkmR_2, newdata = pred_df)
conc_nlme_3 <- predict(pkmR, newdata = pred_df)
pred_df_all <- pred_df[c("Subject", "Dose", "Time")]
pred_df_all <- rbind(
data.frame(pred_df_all, conc = conc_nlm, model = "NLM"),
data.frame(pred_df_all, conc = conc_nlme_2, model = "NLME(2)"),
data.frame(pred_df_all, conc = conc_nlme_3, model = "NLME(3)"))
fig_theoph +
geom_line(data = pred_df_all, aes(Time, conc, color = model))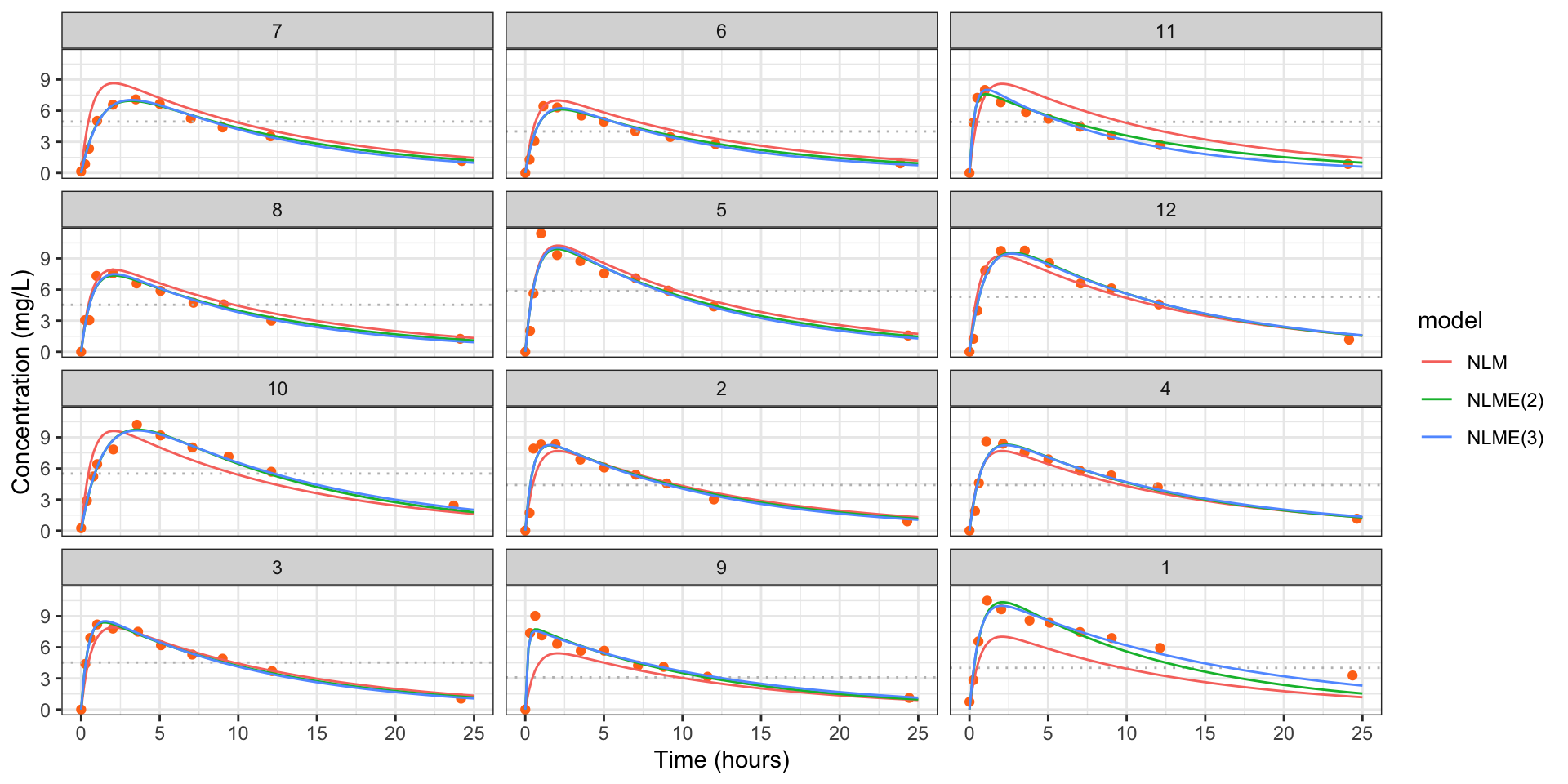
Figure 6: Estimated concentrations for each individual in the theopylline study from model (NLM), model with two effects varying (NLME(2)) and the model with all effects varying (NLM(3)). The dotted line is the administered dose.
Generalized nonlinear mixed effects models
Generalized nonlinear mixed effects models
The generalized nonlinear mixed effects model (GNLMM) assumes \[ Y_i \mid x_i, b_i \stackrel{\text{ind}}{\sim}\mathop{\mathrm{EF}}(\mu_i,\sigma^2)\,, \quad \begin{bmatrix} g(\mu_1)\\\vdots \\ g(\mu_n) \end{bmatrix} = \eta(\beta + A b_i, x_i) \,, \quad b_i \stackrel{\text{ind}}{\sim}{\mathop{\mathrm{N}}}(0,\Sigma_b) \] where \(\mathop{\mathrm{EF}}(\mu_i,\sigma^2)\) is an exponential family with mean \(\mu_i\) and variance \(\sigma^2 V(\mu_i) / m_i\).
Special cases
Linear model, nonlinear model, linear mixed effects model, nonlinear mixed effects model, generalized linear model, and generalized nonlinear model.
Fitting GNLMMs
As in GLMMs, the likelihood function may not have a closed form and needs approximation.
General-purpose optimizers may not converge to a global maximum of the likelihood.
Evaluating \(\eta(\beta, x)\) can be computationally expensive in some applications, like, for example, when \(\eta(\beta, x)\) is defined via a differential equation, which can only be solved numerically.
| Materials | Link |
|---|---|
| Preliminary material | ikosmidis.com/files/APTS-SM-Preliminary |
| Notes | ikosmidis.com/files/APTS-SM-Notes |
| Slides: Introduction | ikosmidis.com/files/APTS-SM-Slides-intro |
| Slides: Model selection | ikosmidis.com/files/APTS-SM-Slides-model-selection |
| Slides: Beyond GLMs | ikosmidis.com/files/APTS-SM-Slides-beyond-glms |
| Slides: Nonlinear models | ikosmidis.com/files/APTS-SM-Slides-nonlinear-models |
| Slides: Latent variables | ikosmidis.com/files/APTS-SM-Slides-latent |
| Lab 1 | ikosmidis.com/files/APTS-SM-Notes/lab1.html |
| Lab 2 | ikosmidis.com/files/APTS-SM-Notes/lab2.html |

Ioannis Kosmidis - Statistical Modelling: Nonlinear models
